题目内容
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=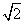 ,
,
(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,若存在,求点M的位置,若不存在,请说明理由。
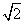 ,
,(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,若存在,求点M的位置,若不存在,请说明理由。

| 解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别 为x,y,z轴建立空间直角坐标系, 则  , ,做BD的中点F并连接CF,AF, 由题意可得CF⊥BD且  , ,又∵平面BDA⊥平面BDC, ∴CF⊥平面BDA, 所以C的坐标为  , ,∴  , ,∴  , ,故DE⊥AC。 (Ⅱ)设平面BCE的法向量为  , ,则  , ,∴  , ,令x=1得,  , ,又  , ,设DE与平面BCE所成角为θ, 则  ; ;(Ⅲ)假设存在点M使得CM∥面ADE, 则  , , , ,∴  ,得 ,得 , ,又因为AE⊥平面ABD,AB⊥BD, 所以AB⊥平面ADE, 因为CM∥面ADE, 则  , ,得  , ,∴  , ,故点M为BE的中点时,CM∥面ADE。 |
 |

练习册系列答案
相关题目
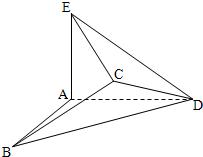 若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).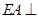 平面ABD,AE=a。
平面ABD,AE=a。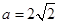 ,求证:AB//平面CDE;
,求证:AB//平面CDE;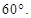
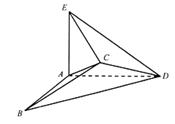
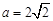 ,求证:AB//平面CDE;
,求证:AB//平面CDE;