题目内容
已知三棱锥A-BCD，三组对棱两两相等，即AB=CD=1，AD=BC=
，AC=BD=
，则三棱锥A-BCD的外接球表面积是
．
| 3 |
| 5 |
| 9π |
| 2 |
| 9π |
| 2 |
分析：由四面体A-BCD相对的棱长度相等，将其放置于长方体中，如图所示．由题意得该长方体的外接球就是四面体A-BCD的外接球，因此算出长方体的对角线长得到外接球的直径，利用球的表面积公式加以计算，可得四面体A-BCD的外接球的表面积．
解答：解：将四面体A-BCD放置于长方体中，如图所示．
∵四面体A-BCD的顶点为长方体八个顶点中的四个，
∴长方体的外接球就是四面体A-BCD的外接球，
∵AB=CD=1，AD=BC=
，AC=BD=
，
∴长方体的对角线长为
=
，
可得外接球的直径2R=
，所以R=
因此，外接球的表面积为S=4πR2=
．
故答案为：
∵四面体A-BCD的顶点为长方体八个顶点中的四个，
∴长方体的外接球就是四面体A-BCD的外接球，
∵AB=CD=1，AD=BC=
| 3 |
| 5 |
∴长方体的对角线长为
|
3
| ||
| 2 |
可得外接球的直径2R=
3
| ||
| 2 |
3
| ||
| 4 |
因此，外接球的表面积为S=4πR2=
| 9π |
| 2 |
故答案为：
| 9π |
| 2 |
点评：本题给出相对棱长相等的四面体，求它的外接球的表面积．着重考查了长方体的性质、长方体的对角线长公式和球的表面积公式等知识，属于中档题．
练习册系列答案
相关题目
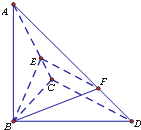已知三棱锥A-BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E，F分别是直线AC，AD上的点，且
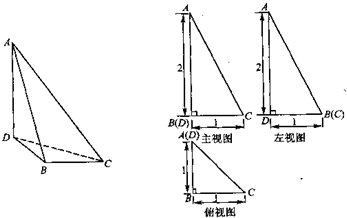（2009•大连一模）已知三棱锥A-BCD及其三视图如图所示．