Question

【题目】过点作圆的两条切线，切点分别为，直线恰好经过椭圆C：的右顶点和上顶点.

（1）求椭圆C方程；

（2）过椭圆C左焦点F的直线l交椭圆C于两点，椭圆上存在一点P，使得四边形为平行四边形，求直线l的方程。

Answer 1

【答案】(1)；(2).

【解析】

（1）由题意可设切线方程为，利用圆心到直线的距离等于半径确定斜率的值可得切线方程，据此确定点N的坐标为，从而可得椭圆方程；

（2）①k不存在或k=0时，在椭圆上不存在点P使得四边形OAPB为平行四边形,

②当k存在且不为0时，设点，设直线l的方程为y=k（x+1），联立直线方程与椭圆方程，结合题意和韦达定理确定直线的斜率即可确定直线l的方程.

（1）过作圆的两条切线，一条切线方程为y=1，切点为M（0，1）.

设另一条切线为，即，

由直线与圆相切，有：，

，解得k=0(舍去)或.

故切线方程为，

由可得：.

可得直线MN的方程为.

由上可知，上顶点坐标为（0，1），右顶点坐标为.

所以椭圆C的方程为.

（2）①k不存在或k=0时，在椭圆上不存在点P使得四边形OAPB为平行四边形,

②当k存在且不为0时，设点，

设直线l的方程为y=k（x+1），

联立直线方程与椭圆方程可得：，

故，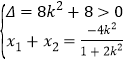

若四边形OAPB为平行四边形，则有：

，

.

又点P在椭圆上，则有，

整理得.

∴直线的方程为.