Question

【题目】已知圆锥的侧面展开图是一个半圆．

（1）求圆锥的母线与底面所成的角；

（2）过底面中心且平行于母线的截平面，若截面与圆锥侧面的交线是焦参数（焦点到准线的距离）为的抛物线，求圆锥的全面积；

（3）过底面点作垂直且于母线的截面，若截面与圆锥侧面的交线是长轴为的椭圆，求椭圆的面积（椭圆号的面积）

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）根据侧面展开图的特征列方程得出底面半径和母线的关系，从而得出母线和底面所成的角；

（2）根据抛物线的一条弦为圆锥底面直径得出底面半径和的关系，从而可得圆锥的面积；

（3）根据三角形相似和圆锥的特点得出椭圆的长轴，短轴和底面半径的关系，从而可得长短轴的关系，得出答案.

（1）设圆锥的底面半径为，母线长为，则圆锥侧面展开图的半径为，弧长为，

圆锥的侧面展开图是一个半圆，

，，

圆锥的轴截面为等边三角形，

圆锥的母线与底面所成的角为；

（2）设抛物线的顶点为，

截面，

则为的中点，

设抛物线方程为，把代入抛物线方程得，

，于是母线，

又由（1）可知，即，，

圆锥的全面积为；

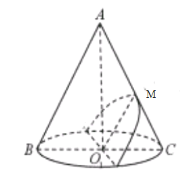
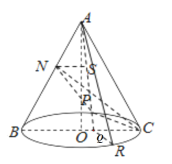
（3）设的中点为，则和为椭圆的长轴顶点，

取的中点，则为椭圆的中心，连接并延长，交于，过作，交圆锥底面圆周于，

则，即，

过作交于，由可知，又，

为靠近的三等分点，连接， ，

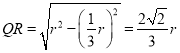中，根据余弦定理

，

，，，

中，过点平行于的线段是，

，，即，

所以椭圆面积