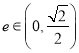题目内容
【题目】已知函数![]() ,
,![]() 、
、![]() 、
、![]() ,且
,且![]() 都有
都有![]() ,满足
,满足![]() 的实数
的实数![]() 有且只有
有且只有![]() 个,给出下述四个结论:
个,给出下述四个结论:
①满足题目条件的实数![]() 有且只有
有且只有![]() 个;②满足题目条件的实数
个;②满足题目条件的实数![]() 有且只有
有且只有![]() 个;
个;
③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() .
.
其中所有正确结论的编号是( )
A.①④B.②③C.①②③D.①③④
【答案】D
【解析】
设![]() ,由
,由![]() ,得出
,得出![]() ,由题意得出
,由题意得出![]() 为函数
为函数![]() 的最小值,
的最小值,![]() 为函数
为函数![]() 的最大值,作出函数
的最大值,作出函数![]() 的图象,结合图象得出
的图象,结合图象得出![]() ,进而对各结论进行验证.
,进而对各结论进行验证.
![]() ,当
,当![]() 时,
时,![]() .
.
设![]() 进行替换,作出函数
进行替换,作出函数![]() 的图象如下图所示:
的图象如下图所示:

由于函数![]() 在
在![]() 上满足
上满足![]() 的实数
的实数![]() 有且只有
有且只有![]() 个,
个,
即函数![]() 在
在![]() 上有且只有
上有且只有![]() 个零点,
个零点,
由图象可知![]() ,解得
,解得![]() ,结论④正确;
,结论④正确;
由图象知,![]() 在
在![]() 上只有一个最小值点,有一个或两个最大值点,结论①正确,结论②错误;
上只有一个最小值点,有一个或两个最大值点,结论①正确,结论②错误;
当![]()
![]() 时,
时,![]() ,
,
由![]() 知
知![]() ,所以
,所以![]() 在
在![]() 上递增,
上递增,
则函数![]() 在
在![]() 上单调递增,结论③正确.综上,正确的有①③④.故选:D.
上单调递增,结论③正确.综上,正确的有①③④.故选:D.

练习册系列答案
相关题目
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生,新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女生 | 40 | 40 |
(1)通过估算,试判断男、女哪种性别的学生愿意投入到新生接待工作的概率更大.
(2)能否有99%的把握认为,愿意参加新生接待工作与性别有关?
附: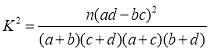 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |