题目内容
13.已知函数f(x)=xlnx+x2-3x-$\frac{x}{e^x}$(x>0)(e为自然对数的底数)(Ⅰ)求f(x)的极值;
(Ⅱ)求证:ex≥x+1;
(Ⅲ)求证f'(x)在(0,+∞)上为单调递增函数.
分析 (Ⅰ)求出函数的导数,判断函数的单调性,然后求解函数的极值.
(Ⅱ)构造函数h(x)=ex-x-1,利用导数求解函数的最值,即可证明ex≥x+1,
(Ⅲ)设$g(x)=f'(x)=lnx+2(x-1)+\frac{x-1}{e^x}$,求出导数,转化证明$\frac{1}{x}+2+\frac{2-x}{e^x}≥0$在(0,+∞)上恒成立,利用分析法证明f'(x)在(0,+∞)上为单调递增函数.
解答 解:(Ⅰ)$f'(x)=lnx+2(x-1)+\frac{x-1}{e^x}$,
可得x>1时,f'(x)>0,f(x)为增函数,
0<x<1时,f'(x)<0,f(x)为减函数,
所以f(x)存在极小值为$f(1)=-2-\frac{1}{e}$;
(Ⅱ)证明:h(x)=ex-x-1,所以h'(x)=ex-1,
当x≥0时,h'(x)≥0,h(x)为增函数,
当x<0时,h'(x)<0,h(x)为减函数,
所以h(x)≥h(0)=0,所以ex≥x+1,
(Ⅲ)证明:设$g(x)=f'(x)=lnx+2(x-1)+\frac{x-1}{e^x}$,
则$g'(x)=\frac{1}{x}+2+\frac{2-x}{e^x}$,欲证f'(x)在(0,+∞)上为单调递增函数,
只需证明$\frac{1}{x}+2+\frac{2-x}{e^x}≥0$在(0,+∞)上恒成立,显然x∈(0,2]符合题意,
当x>2时,只需证明${e^x}≥\frac{{{x^2}-2x}}{2x+1}$.
因为(x+1)(2x+1)-(x2-2x)=x2+5x+1在x>2时大于零,
所以${e^x}≥x+1>\frac{{{x^2}-2x}}{2x+1}$,所以原式得证,
所以f'(x)在(0,+∞)上为单调递增函数.
点评 本题考查函数的导数的综合应用,考查转化思想以及计算能力,构造法的应用,函数的最值的求法,难度比较大,

| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
| A. | 36 | B. | 42 | C. | 48 | D. | 60 |
| X | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{4}$ | m |
| A. | $\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ | B. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ |
| A. | (¬p)∧(¬q) | B. | p∧q | C. | (¬p)∧p) | D. | (p)∨q |
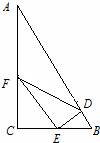 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米,现在准备养一批供游客观赏的鱼,分别在AB,BC,CA上取点D,E,F,如图,使得EF∥AB,EF⊥ED,在△DEF喂食,求S△DEF的最大值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米,现在准备养一批供游客观赏的鱼,分别在AB,BC,CA上取点D,E,F,如图,使得EF∥AB,EF⊥ED,在△DEF喂食,求S△DEF的最大值.