题目内容
已知元素为实数的集合S满足下列条件:①1、0∉S;②若a∈S,则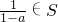
(1)若{2,-2}⊆S,求使元素个数最少的集合S;
(2)若非空集合S为有限集,则你对集合S的元素个数有何猜测?并请证明你的猜测正确.
解: ;
;

∴使{2,-2}?S的元素个数最少的集合S为
(2)设a∈S,则a≠0,1且 (*)
(*)
由于 ,但a2-a+1=0无实数根
,但a2-a+1=0无实数根
故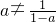 同理
同理 ∴
∴
若存在b∈S,而 ,则
,则 且
且
(若 中有元素∈
中有元素∈ ,
,
则利用前述的(*)式可知b∈ )
)
于是
上述推理还可继续,由于S为有限集,故上述推理有限步可中止
∴S的元素个数为3的倍数.
分析:(1)根据条件若a∈S,则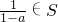 ,分别利用2,-2∈S,进行推导.(2)要使非空集合S为有限集,则集合元素具备一定规律性,利用规律性进行判断.
,分别利用2,-2∈S,进行推导.(2)要使非空集合S为有限集,则集合元素具备一定规律性,利用规律性进行判断.
点评:本题主要考查集合元素的确定,利用条件进行推导元素是解决本题的关键,考查学生的推理和分析能力.
 ;
;
∴使{2,-2}?S的元素个数最少的集合S为

(2)设a∈S,则a≠0,1且
 (*)
(*)由于
 ,但a2-a+1=0无实数根
,但a2-a+1=0无实数根故
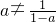 同理
同理 ∴
∴
若存在b∈S,而
 ,则
,则 且
且
(若
 中有元素∈
中有元素∈ ,
,则利用前述的(*)式可知b∈
 )
)于是

上述推理还可继续,由于S为有限集,故上述推理有限步可中止
∴S的元素个数为3的倍数.
分析:(1)根据条件若a∈S,则
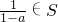 ,分别利用2,-2∈S,进行推导.(2)要使非空集合S为有限集,则集合元素具备一定规律性,利用规律性进行判断.
,分别利用2,-2∈S,进行推导.(2)要使非空集合S为有限集,则集合元素具备一定规律性,利用规律性进行判断.点评:本题主要考查集合元素的确定,利用条件进行推导元素是解决本题的关键,考查学生的推理和分析能力.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目

 则
则 那么集合A中所有元素的乘积为( )
那么集合A中所有元素的乘积为( ) C.
1
D. -1
C.
1
D. -1 ,那么集合A中所有元素的乘积为( )
,那么集合A中所有元素的乘积为( )