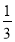题目内容
1.已知直线l1:12x-5y+15=0和l2:x=-2,点P为抛物线y2=8x上的动点,则点P到直线l1和直线l2的距离之和的最小值为3.分析 由抛物线方程求出其焦点坐标和准线方程,把抛物线y2=8x上的点P到两直线l1:x=-2,l2:12x-5y+15=0的距离之和的最小值转化为焦点到l2:12x-5y+15=0的距离,由点到直线的距离公式求解.
解答 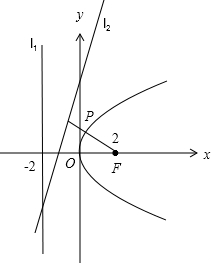 解:如图,
解:如图,
由抛物线y2=8x,得其焦点F(2,0),准线方程为x=-2.
∴l1:x=-2为抛物线的准线,
P到两直线l1:x=-2,l2:12x-5y+15=0的距离之和,
即为P到F和l2:12x-5y+15=0的距离之和.
最小值为F到l2:12x-5y+15=0的距离$d=\frac{{|{12×2+15}|}}{{\sqrt{{{12}^2}+{5^2}}}}=3$.
故答案为:3.
点评 本题考查了直线与圆锥曲线的关系,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
相关题目
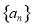 的前
的前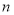 项和为
项和为 ,且
,且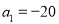 .在区间
.在区间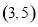 内任取一个实数作为数列
内任取一个实数作为数列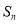 的最小值仅为
的最小值仅为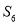 的概率为( )
的概率为( )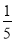 B.
B.
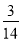 D.
D.