题目内容
16.已知a>0,b>0.(I)若a+b=2,求$\frac{1}{1+a}+\frac{4}{1+b}$的最小值;
(Ⅱ)求证:a2b2+a2+b2≥ab(a+b+1).
分析 (Ⅰ)运用乘1法,可得$\frac{1}{1+a}+\frac{4}{1+b}$=$\frac{1}{4}$($\frac{1}{1+a}+\frac{4}{1+b}$)(1+a+1+b),展开后运用基本不等式即可得到最小值;
(Ⅱ)运用均值不等式,结合累加法,即可得证.
解答 解:(Ⅰ)由于a+b=2,
则$\frac{1}{1+a}+\frac{4}{1+b}$=$\frac{1}{4}$($\frac{1}{1+a}+\frac{4}{1+b}$)(1+a+1+b)
=$\frac{1}{4}$(5+$\frac{1+b}{1+a}$+$\frac{4(1+a)}{1+b}$)≥$\frac{1}{4}$(5+2$\sqrt{\frac{1+b}{1+a}•\frac{4+4a}{1+b}}$)=$\frac{9}{4}$
等号成立条件为$\frac{1+b}{1+a}$=$\frac{4(1+a)}{1+b}$,而a+b=2,所以a=$\frac{1}{3}$,b=$\frac{5}{3}$,
因此当a=$\frac{1}{3}$,b=$\frac{5}{3}$时,$\frac{1}{1+a}$+$\frac{4}{1+b}$取得最小值,且为$\frac{9}{4}$;
(Ⅱ)证明:由均值不等式得a2b2+a2≥2a2b,a2b2+b2≥2b2a,a2+b2≥2ab
三式相加得2a2b2+2a2+2b2≥2a2b+2ab2+2ab=2ab(a+b+1),
所以a2b2+a2+b2≥ab(a+b+1).
点评 本题考查基本不等式的运用:求最值和证明不等式,注意运用乘1法和累加法是解题的关键.

练习册系列答案
相关题目
5.函数f(x)=x•e|x|的大致图象为( )
| A. |  | B. |  | C. |  | D. |  |
6. 在△ABC中,∠CAB=∠CBA=30°,AC,BC边上的高分别为BD,AE,则以A,B为焦点,且过D,E两点的椭圆和双曲线的离心率的乘积为( )
在△ABC中,∠CAB=∠CBA=30°,AC,BC边上的高分别为BD,AE,则以A,B为焦点,且过D,E两点的椭圆和双曲线的离心率的乘积为( )
 在△ABC中,∠CAB=∠CBA=30°,AC,BC边上的高分别为BD,AE,则以A,B为焦点,且过D,E两点的椭圆和双曲线的离心率的乘积为( )
在△ABC中,∠CAB=∠CBA=30°,AC,BC边上的高分别为BD,AE,则以A,B为焦点,且过D,E两点的椭圆和双曲线的离心率的乘积为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
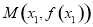 和点
和点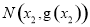 分别是函数
分别是函数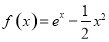 和
和 图象上的点,且
图象上的点,且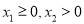 .若直线
.若直线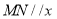 轴,则
轴,则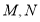 两点间的距离的最小值为( )
两点间的距离的最小值为( )