题目内容
(2006
·北京)已知点M(－2，0)，N(2，0)，动点P满足条件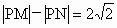
，设动点P的轨迹为W．
(1)
求W的方程；(2)
若A，B是W上的不同两点，O是坐标原点，求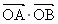
的最小值．
答案：略
解析：
解析：
|
解法一： (1) 由 知动点P的轨迹是以M，N为焦点的双曲线的右支，实半轴长 ．
又半焦距 c=2，故虚半轴长 ．
所以 W的方程为 ．
(2) 设A，B的坐标分别为 ， ．
当  轴时， ，从而 ，
当 AB不与x轴垂直时，设直线AB的方程为y=kx＋m，与W的方程联立，消去y得
故  ，所以
又因为  ，所以 ，从而 ．
综上，当 轴时， 取得最小值2．
解法二： (1) 同解法一．(2) 设A，B的坐标分别为， ，，则
 ， ，则 ，且 ．所以
当且仅当  ，即 时“=”成立．
所以 的最小值是2． |
练习册系列答案
相关题目
(2006
北京东城模拟)已知直线y=2x上一点P的横坐标为a，有两个点A(－1，1)，B(3，3)，那么使向量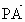
与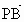
夹角为钝角的一个充分但不必要的条件是
[
]|
A ．－1＜a＜2 |
B ．0＜a＜1 |
|
C ． |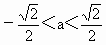
D ．0＜a＜2 |
(2006
北京东城模拟)已知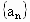
是首项为1，公比为q的等比数列，
．
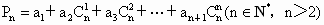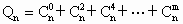
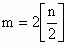，[t]表示不大于t的最大整数，例如[2.5]=2）．如果数列
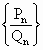有极限，那么公比q的取值范围是
[
]|
A ．－1＜q≤1，且q≠0 |
B ．－1＜q＜1，且q≠0 |
|
C ．－3＜q≤1，且q≠0 |
D ．－3＜q＜1，且q≠0 |
(2006
北京东城模拟)在△ABC中，已知sinC=2sin(B＋C)cosB，那么△ABC一定是[
]|
A ．等腰直角三角形 |
B ．等腰三角形 |
|
C ．直角三角形 |
D ．等边三角形 |
(2006
北京崇文模拟)已知
，则
的值为
[
]|
A ． |
B ． |
C ． |
D ． |
．
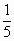