题目内容
【题目】已知函数![]() 在
在![]() 处取得极小值.
处取得极小值.
(1)求实数![]() 的值;
的值;
(2)设![]() ,其导函数为
,其导函数为![]() ,若
,若![]() 的图象交
的图象交![]() 轴于两点
轴于两点![]() 且
且![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,试问
,试问![]() 是否为
是否为![]() 的根?说明理由.
的根?说明理由.
【答案】(1)![]() (2)
(2)![]() 不是
不是![]() 的根.
的根.
【解析】试题分析:(1)先求导数,再根据![]() ,解得
,解得![]() ,最后列表验证(2)即研究
,最后列表验证(2)即研究![]() 是否成立,因为
是否成立,因为![]() ,利用
,利用![]() ,
,
![]() 得
得![]() ,所以
,所以![]() =0,转化为
=0,转化为![]() .其中
.其中![]() ,最后利用导数研究函数
,最后利用导数研究函数![]() 单调性,确定方程解的情况
单调性,确定方程解的情况
试题解析:(1)因为![]() ,
,
所以![]() ,
,
因为函数![]() 在
在![]() 处取得极小值,
处取得极小值,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() 在
在![]() 处取得极小值,符合题意.
处取得极小值,符合题意.
所以![]() .
.
(2)由(1)知函数![]() .
.
∵函数![]() 图象与
图象与![]() 轴交于两个不同的点
轴交于两个不同的点![]() ,(
,( ![]() ),
),
∴![]() ,
,
![]() .
.
两式相减得
![]()
![]() .
.
![]() .
.
下解![]() .
.
即![]() .
.
令![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
即![]() .
.
令![]() ,
,
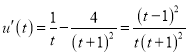 .
.
又![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上是増函数,则
上是増函数,则![]() ,
,
从而知![]() ,
,
故![]() ,即
,即![]() 不成立.
不成立.
故![]() 不是
不是![]() 的根.
的根.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
