题目内容
已知平面向量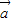
=（1，2），
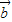=（-2，m），且
∥
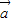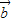，则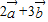
=（ ）A．（-5，-10）
B．（-4，-8）
C．（-3，-6）
D．（-2，-4）
【答案】分析：向量平行的充要条件的应用一种做法是根据平行求出向量的坐标，然后用向量线性运算得到结果；另一种做法是针对选择题的特殊做法，即排除法．
解答：解：排除法：横坐标为2+（-6）=-4，
故选B．
点评：认识向量的代数特性．向量的坐标表示，实现了“形”与“数”的互相转化．以向量为工具，几何问题可以代数化，代数问题可以几何化．
解答：解：排除法：横坐标为2+（-6）=-4，
故选B．
点评：认识向量的代数特性．向量的坐标表示，实现了“形”与“数”的互相转化．以向量为工具，几何问题可以代数化，代数问题可以几何化．
练习册系列答案
相关题目
已知平面向量
=（1，2），
=（-2，m），且
∥
，则m的值为（ ）
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、4 | D、-4 |
已知平面向量
=（1，2），
=（-2，m），且
∥
，则|
|=（ ）
| a |
| b |
| a |
| b |
| b |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知平面向量
=（1，-2），
=（2，1），
=（-4，-2），则下列结论中错误的是（ ）
| a |
| b |
| c |
A、向量
| ||||||||
B、若
| ||||||||
C、对同一平面内任意向量
| ||||||||
D、向量
|