题目内容
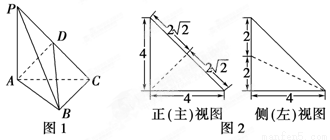
如图1，在三棱锥P－ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上一点，它的正(主)视图和侧(左)视图如图2所示．
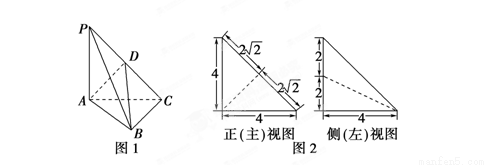
(1)证明：AD⊥平面PBC；
(2)求三棱锥D－ABC的体积；
(3)在∠ACB的平分线上确定一点Q，使得PQ∥平面ABD，并求此时PQ的长．
【答案】
(1)
………………4分
(2) 
……………………………………8分
(3)取AB的中点O，连接CO并延长至Q，使得CQ＝2CO，
连接PQ，OD，点Q即为所求．
因为O为CQ的中点，D为PC的中点，
PQ
OD,
PQ
平面ABD, OD
平面ABD
PQ平面ABD
连接AQ,BQ,
四边形ACBQ的对角线互相平分，且AC=BC,AC
BC,
四边形ACBQ为正方形，
CQ即为∠ACB的平分线
又AQ=4，PA平面ABC
在直角三角形PAQ中，PQ=
【解析】略
练习册系列答案
相关题目
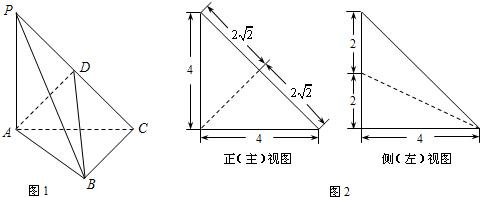
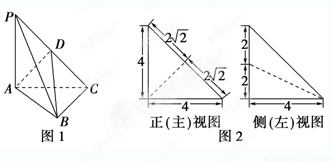
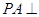平面ABC，
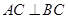，D为侧棱PC上一点，它的正（主）视图和侧（左）视图如图2所示。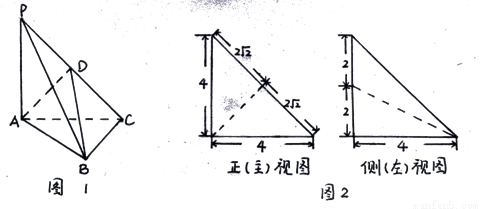
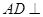平面PBC；
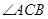的平分线上确定一点Q，使得
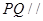平面ABD，并求此时PQ的长。