题目内容
 如图,AC、BC分别是直角三角形ABC的两条直角边,且AC=3,BC=4,以AC为直径作圆与斜边AB交于D,则BD=________.
如图,AC、BC分别是直角三角形ABC的两条直角边,且AC=3,BC=4,以AC为直径作圆与斜边AB交于D,则BD=________.

分析:做出辅助线连CD,先在Rt△ABC中利用勾股定理求出AB=5cm,再利用两个直角三角形相似Rt△BDC∽Rt△BCA,代入数据求出BD的值.
解答:连CD,
在Rt△ABC中,因为AC、BC的长分别为3cm、4cm,所以AB=5cm,
∵AC为直径,
∴∠ADC=90°,
∵∠B公共角,
可得Rt△BDC∽Rt△BCA,
∴BD=
 ,
,故答案为:

点评:本题考查了圆周角定理.直径所对的圆周角为90度.考查了勾股定理以及三角形相似的判定与性质,本题解题的关键是把要求的线段放到可解的三角形中,根据三角形的性质来解题.

练习册系列答案
相关题目
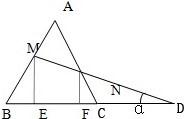 (如图)CD是BC的延长线,AB=BC=CA=CD=a,DM与AB,AC分别交于M点和N点,且∠BDM=α.
(如图)CD是BC的延长线,AB=BC=CA=CD=a,DM与AB,AC分别交于M点和N点,且∠BDM=α.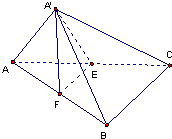 如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A'EF的位置,使A′C=
如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A'EF的位置,使A′C=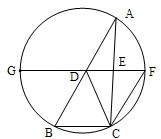 (2012•黑龙江)选修4-1:几何证明选讲
(2012•黑龙江)选修4-1:几何证明选讲 如图,AC为圆O的直径,AP⊥圆O,PA=AB=BC.
如图,AC为圆O的直径,AP⊥圆O,PA=AB=BC. (几何证明选讲选选做题)如图,AC是⊙O的直径,B是⊙O上一点,∠ABC的平分线与⊙O相交于.D已知BC=1,AB=
(几何证明选讲选选做题)如图,AC是⊙O的直径,B是⊙O上一点,∠ABC的平分线与⊙O相交于.D已知BC=1,AB=