题目内容
定义:min{x,y}为实数x,y中较小的数.已知h=min {a,
},其中a,b 均为正实数,则h的最大值是
.
| b |
| a2+4b2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:由于a,b 均为正实数,
=
≤
,比较a与
的大小即可求得h的最大值.
| b |
| a2+4b2 |
| 1 | ||
|
| 1 |
| 4a |
| 1 |
| 4a |
解答:解:∵a,b 均为正实数,
=
≤
,
∴当a≥
,即a≥
时,
≤
,即
≤
,
∴h=min{a,
}=
≤
;
当0<a<
时,h=min{a,
}<
;
综上所述,h的最大值为
.
故答案为:
.
| b |
| a2+4b2 |
| 1 | ||
|
| 1 |
| 4a |
∴当a≥
| 1 |
| 4a |
| 1 |
| 2 |
| 1 |
| 4a |
| 1 |
| 2 |
| b |
| a2+4b2 |
| 1 |
| 2 |
∴h=min{a,
| b |
| a2+4b2 |
| b |
| a2+4b2 |
| 1 |
| 2 |
当0<a<
| 1 |
| 2 |
| b |
| a2+4b2 |
| 1 |
| 2 |
综上所述,h的最大值为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查不等式比较大小,关键在于利用基本不等式求得
≤
,再对a与
的大小进行比较,分析转化与运算的能力,属于难题.
| b |
| a2+4b2 |
| 1 |
| 4a |
| 1 |
| 4a |

练习册系列答案
相关题目
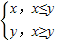 ,已知函数g(x)=min{(
,已知函数g(x)=min{( )x,2x+1},则g(x)的最大值为 .
)x,2x+1},则g(x)的最大值为 . ,已知函数g(x)=min{(
,已知函数g(x)=min{( )x,2x+1},则g(x)的最大值为 .
)x,2x+1},则g(x)的最大值为 . ,其中a,b 均为正实数,则h的最大值是 .
,其中a,b 均为正实数,则h的最大值是 .