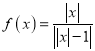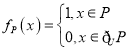题目内容
【题目】已知数列1、1、2、1、2、4、1、2、4、8、1、2、4、8、16、…，其中第一项是
，接下来的两项是、
，再接下来的三项是、、
，以此类推，若
且该数列的前
项和为2的整数幂，则的最小值为（ ）
A.440B.330C.220D.110
【答案】A
【解析】
把题设中的数列分成如下的组：
，记前
组的和为
，算出后结合前
项和为2的整数幂可得的最小值.
把题设中的数列分成如下的组： ，记前组的和为。
则
.
令
即
，故
.
故当
时，数列至少包括前13组且含有第14组的前
个元素.
设前项和为2的整数幂且第项为第组的第
个元素，则
，
且前项和
，其中
，.
下证：当时，总有
.
记
，则当时，有
，
故
为单调增数列，而
，故
即.
所以
，
由
为2的整数幂，故
，从而
，
当
时，
，与
矛盾；
当
时，
，此时
，
故选：A.
练习册系列答案
全优点练单元计划系列答案
相关题目
