题目内容
设函数f(x)=|2x-m|+4x.
(I)当m=2时,解不等式:f(x)≤1;
(Ⅱ)若不等式f(x)≤2的解集为{x|x≤-2},求m的值.
解:(I)当m=2时,函数f(x)=|2x-2|+4x,由不等式f(x)≤1 可得 ①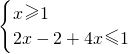 ,或 ②
,或 ②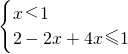 .
.
解①可得x∈∅,解②可得x≤- ,故不等式的解集为 {x|x≤-
,故不等式的解集为 {x|x≤- }.
}.
(Ⅱ)∵f(x)=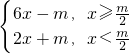 ,连续函数f(x) 在R上是增函数,由于f(x)≤2的解集为{x|x≤-2},
,连续函数f(x) 在R上是增函数,由于f(x)≤2的解集为{x|x≤-2},
故f(-2)=2,当 ≥-2时,有2×(-2)+m=2,解得 m=6.
≥-2时,有2×(-2)+m=2,解得 m=6.
当 <-2时,则有6×(-2)-m=2,解得 m=-14.
<-2时,则有6×(-2)-m=2,解得 m=-14.
综上可得,当 m=6或 m=-14 时,f(x)≤2的解集为{x|x≤-2}.
分析:(I)当m=2时,函数f(x)=|2x-2|+4x,由不等式f(x)≤1 可得 ①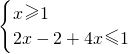 ,或 ②
,或 ②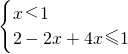 ,分别求出①②的解集,再取并集,即得所求.
,分别求出①②的解集,再取并集,即得所求.
(Ⅱ)由f(x)=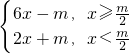 ,可得连续函数f(x) 在R上是增函数,故有f(-2)=2,分当
,可得连续函数f(x) 在R上是增函数,故有f(-2)=2,分当 ≥-2和当
≥-2和当 <-2两种情况,分别求出m的值,即为所求.
<-2两种情况,分别求出m的值,即为所求.
点评:本题主要考查带有绝对值的函数,绝对值不等式的解法,体现了分类讨论的数学思想,属于中档题.
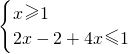 ,或 ②
,或 ②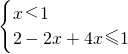 .
.解①可得x∈∅,解②可得x≤-
 ,故不等式的解集为 {x|x≤-
,故不等式的解集为 {x|x≤- }.
}.(Ⅱ)∵f(x)=
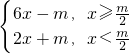 ,连续函数f(x) 在R上是增函数,由于f(x)≤2的解集为{x|x≤-2},
,连续函数f(x) 在R上是增函数,由于f(x)≤2的解集为{x|x≤-2},故f(-2)=2,当
 ≥-2时,有2×(-2)+m=2,解得 m=6.
≥-2时,有2×(-2)+m=2,解得 m=6.当
 <-2时,则有6×(-2)-m=2,解得 m=-14.
<-2时,则有6×(-2)-m=2,解得 m=-14.综上可得,当 m=6或 m=-14 时,f(x)≤2的解集为{x|x≤-2}.
分析:(I)当m=2时,函数f(x)=|2x-2|+4x,由不等式f(x)≤1 可得 ①
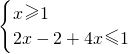 ,或 ②
,或 ②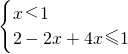 ,分别求出①②的解集,再取并集,即得所求.
,分别求出①②的解集,再取并集,即得所求.(Ⅱ)由f(x)=
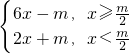 ,可得连续函数f(x) 在R上是增函数,故有f(-2)=2,分当
,可得连续函数f(x) 在R上是增函数,故有f(-2)=2,分当 ≥-2和当
≥-2和当 <-2两种情况,分别求出m的值,即为所求.
<-2两种情况,分别求出m的值,即为所求.点评:本题主要考查带有绝对值的函数,绝对值不等式的解法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目