题目内容
若P（a，b）是双曲线x2-4y2=m（m≠0）上一点，且满足a-2b＞0，a+2b＞0，则该点一定位于双曲线
- A.右支上
- B.上支上
- C.右支上或上支上
- D.不能确定
A
分析：把点P的坐标代入双曲线方程，根据题设可求得m大于0，判断出双曲线的焦点在x轴上，进而根据题设不等式可求得a＞0，进而可推断出点P在右支上．
解答：∵P是双曲线上的点，代入双曲线方程得
a2-4b2=（a-2b）（a+2b）=m
∵a-2b＞0，a+2b＞0，∴m＞0
∴双曲线的焦点在x轴上，
∵a-2b＞0，a+2b＞0，
∴2a＞0，a＞0
∴P点在y轴的右侧，只能在双曲线的右支上．
故选A
点评：本题主要考查了双曲线的简单性质．考查了学生对双曲线方程和简单性质的掌握．
分析：把点P的坐标代入双曲线方程，根据题设可求得m大于0，判断出双曲线的焦点在x轴上，进而根据题设不等式可求得a＞0，进而可推断出点P在右支上．
解答：∵P是双曲线上的点，代入双曲线方程得
a2-4b2=（a-2b）（a+2b）=m
∵a-2b＞0，a+2b＞0，∴m＞0
∴双曲线的焦点在x轴上，
∵a-2b＞0，a+2b＞0，
∴2a＞0，a＞0
∴P点在y轴的右侧，只能在双曲线的右支上．
故选A
点评：本题主要考查了双曲线的简单性质．考查了学生对双曲线方程和简单性质的掌握．
练习册系列答案
备战中考寒假系列答案
相关题目
已知F1，F2分别为双曲
-
=1(a＞0，b＞0)的左、右焦点，P为双曲线左支上任一点，若
的最小值为8a，则双曲线的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、（1，+∞） |
| B、（0，3] |
| C、（1，3] |
| D、（0，2] |
一条渐近线的方程是
过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点，R是弦PQ的中点.
|F1F2|，求线段AB的中点M的迹方程，并说明该轨迹是什么曲线。
，当点P在曲线C上运动时，求a的取值范围.
为坐标原点，
,
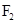是双曲线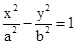
（a＞0，b＞0）的焦点，若在双曲
,则该双曲线的渐近线方程为(
)
y=0
B.
=0 D.
±y=0
的左、右焦点，P为双曲线左支上任一点，若
的最小值为8a，则双曲线的离心率e的取值范围是（ ）