题目内容
已知△AOB的顶点A在射线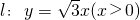 上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l上移动时,记点M的轨迹为W.
上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l上移动时,记点M的轨迹为W.
(Ⅰ)求轨迹W的方程;
(Ⅱ)设P(-1,0),Q(2,0),求证:∠MQP=2∠MPQ.
(Ⅰ)解:因为A,B两点关于x轴对称,
所以AB边所在直线与y轴平行.
设M(x,y),由题意,得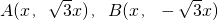 ,
,
所以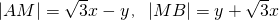 ,
,
因为|AM|•|MB|=3,
所以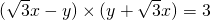 ,即
,即 ,
,
所以点M的轨迹W的方程为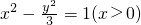 .
.
(Ⅱ)证明:设M(x0,y0)(x0>0),
因为曲线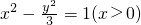 关于x轴对称,
关于x轴对称,
所以只要证明“点M在x轴上方及x轴上时,∠MQP=2∠MPQ”成立即可.
以下给出“当y0≥0时,∠MQP=2∠MPQ”的证明过程.
因为点M在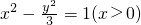 上,所以x0≥1.
上,所以x0≥1.
当x0=2时,由点M在W上,得点M(2,3),
此时MQ⊥PQ,|MQ|=3,|PQ|=3,
所以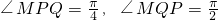 ,则∠MQP=2∠MPQ;
,则∠MQP=2∠MPQ;
当x0≠2时,直线PM、QM的斜率分别为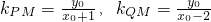 ,
,
因为x0≥1,x0≠2,y0≥0,所以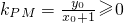 ,且
,且 ,
,
又tan∠MPQ=kPM,所以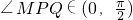 ,且
,且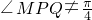 ,
,
所以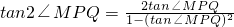 =
=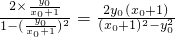 ,
,
因为点M在W上,所以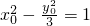 ,即y02=3x02-3,
,即y02=3x02-3,
所以tan2∠MPQ=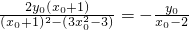 ,
,
因为tan∠MQP=-kQM,
所以tan∠MQP=tan2∠MPQ,
在△MPQ中,因为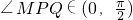 ,且
,且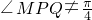 ,∠MQP∈(0,π),
,∠MQP∈(0,π),
所以∠MQP=2∠MPQ.
综上,得当y0≥0时,∠MQP=2∠MPQ.
所以对于轨迹W的任意一点M,∠MQP=2∠MPQ成立.
分析:(Ⅰ)由A,B两点关于x轴对称,得到AB边所在直线与y轴平行.设M(x,y),由题意得出x,y之间的关系即为点M的轨迹W的方程.
(Ⅱ)先设M(x0,y0)(x0>0),因为曲线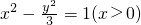 关于x轴对称,所以只要证明“点M在x轴上方及x轴上时,∠MQP=2∠MPQ”成立即可.
关于x轴对称,所以只要证明“点M在x轴上方及x轴上时,∠MQP=2∠MPQ”成立即可.
点评:本小题主要考查直线与圆锥曲线的综合问题、双曲线方程等基础知识,考查运算求解能力、化归思想.属于中档题.
所以AB边所在直线与y轴平行.
设M(x,y),由题意,得
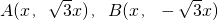 ,
,所以
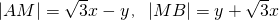 ,
,因为|AM|•|MB|=3,
所以
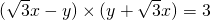 ,即
,即 ,
,所以点M的轨迹W的方程为
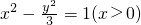 .
.(Ⅱ)证明:设M(x0,y0)(x0>0),
因为曲线
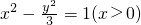 关于x轴对称,
关于x轴对称,所以只要证明“点M在x轴上方及x轴上时,∠MQP=2∠MPQ”成立即可.
以下给出“当y0≥0时,∠MQP=2∠MPQ”的证明过程.
因为点M在
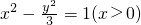 上,所以x0≥1.
上,所以x0≥1.当x0=2时,由点M在W上,得点M(2,3),
此时MQ⊥PQ,|MQ|=3,|PQ|=3,
所以
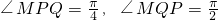 ,则∠MQP=2∠MPQ;
,则∠MQP=2∠MPQ;当x0≠2时,直线PM、QM的斜率分别为
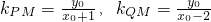 ,
,因为x0≥1,x0≠2,y0≥0,所以
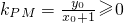 ,且
,且 ,
,又tan∠MPQ=kPM,所以
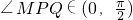 ,且
,且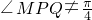 ,
,所以
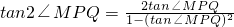 =
=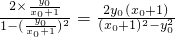 ,
,因为点M在W上,所以
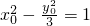 ,即y02=3x02-3,
,即y02=3x02-3,所以tan2∠MPQ=
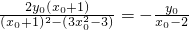 ,
,因为tan∠MQP=-kQM,
所以tan∠MQP=tan2∠MPQ,
在△MPQ中,因为
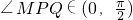 ,且
,且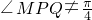 ,∠MQP∈(0,π),
,∠MQP∈(0,π),所以∠MQP=2∠MPQ.
综上,得当y0≥0时,∠MQP=2∠MPQ.
所以对于轨迹W的任意一点M,∠MQP=2∠MPQ成立.
分析:(Ⅰ)由A,B两点关于x轴对称,得到AB边所在直线与y轴平行.设M(x,y),由题意得出x,y之间的关系即为点M的轨迹W的方程.
(Ⅱ)先设M(x0,y0)(x0>0),因为曲线
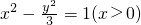 关于x轴对称,所以只要证明“点M在x轴上方及x轴上时,∠MQP=2∠MPQ”成立即可.
关于x轴对称,所以只要证明“点M在x轴上方及x轴上时,∠MQP=2∠MPQ”成立即可.点评:本小题主要考查直线与圆锥曲线的综合问题、双曲线方程等基础知识,考查运算求解能力、化归思想.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
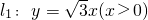 上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l1上移动时,记点M的轨迹为W.
上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l1上移动时,记点M的轨迹为W.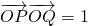 .
.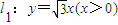 上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l1上移动时,记点M的轨迹为W.
上,A,B两点关于x轴对称,O为坐标原点,且线段AB上有一点M满足|AM|•|MB|=3.当点A在l1上移动时,记点M的轨迹为W.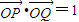 .
.