题目内容
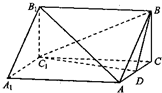 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,D为AC的中点.
(1)求证:AB1∥面BDC1;
(2)若AA1=3,求二面角C1-BD-C的余弦值;
(3)若在线段AB1上存在点P,使得CP⊥面BDC1,试求AA1的长及点P的位置.
证明: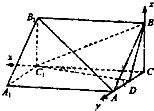 (1)连接B1C,交BC1于点O,
(1)连接B1C,交BC1于点O,
则O为B1C的中点,∵D为AC中点,∴OD∥B1A,又B1A?平面BDC1,OD⊆平面BDC1
∴B1A∥BDC1 (3分)
解:(2)∵AA1⊥平面ABC,BC⊥AC,AA1∥CC1,∴CC1⊥面ABC,
则BC⊥平面AC1,CC1⊥AC
如图建系,则C1(3,0,0),B(0,0,2),D(0,1,0),C(0,0,0)
∴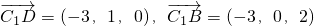
设平面C1DB的法向量为n=(x,y,z)则n=(2,6,3)
又平面BDC的法向量为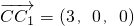 ∴二面角C1-BD-C的余弦值:
∴二面角C1-BD-C的余弦值:
 (8分)
(8分)
(3)设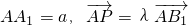 ,
,
∴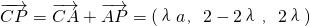
又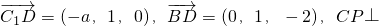 面BDC1,
面BDC1,
∴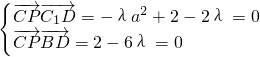 解得
解得
所以AA1=2,点P位置是在线段AB1上且 .(12分)
.(12分)
分析:(1)连接B1C,交BC1于点O,由三角形中位线定理,可得OD∥B1A,结合线面平行的判定定理可得AB1∥面BDC1;
(2)以C为坐标原点,CC1,CA,CB方向分别为X,Y,Z轴正方向建立空间坐标系,求出平面C1DB的法向量和平面BDC的法向量,代入向量夹角公式,即可求出二面角C1-BD-C的余弦值;
(3)设设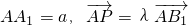 ,求出CP的方向向量和平面BDC1的法向量,根据CP⊥面BDC1,构造关于a,λ的方程组,解方程组,求出a,λ的值,即可得到AA1的长及点P的位置.
,求出CP的方向向量和平面BDC1的法向量,根据CP⊥面BDC1,构造关于a,λ的方程组,解方程组,求出a,λ的值,即可得到AA1的长及点P的位置.
点评:本题考查的知识点是用空间向量求平面间的夹角,直线与平面平行的判定,直线与平面垂直的判定,其中(1)的关键是证得OD∥B1A,(2)(3)的关键是建立空间坐标系,将空间直线与平面的垂直关系及二面角问题转化为空间向量的夹角问题.
 (1)连接B1C,交BC1于点O,
(1)连接B1C,交BC1于点O,则O为B1C的中点,∵D为AC中点,∴OD∥B1A,又B1A?平面BDC1,OD⊆平面BDC1
∴B1A∥BDC1 (3分)
解:(2)∵AA1⊥平面ABC,BC⊥AC,AA1∥CC1,∴CC1⊥面ABC,
则BC⊥平面AC1,CC1⊥AC
如图建系,则C1(3,0,0),B(0,0,2),D(0,1,0),C(0,0,0)
∴
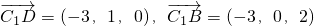
设平面C1DB的法向量为n=(x,y,z)则n=(2,6,3)
又平面BDC的法向量为
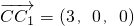 ∴二面角C1-BD-C的余弦值:
∴二面角C1-BD-C的余弦值: (8分)
(8分)(3)设
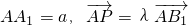 ,
,
∴
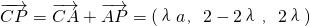
又
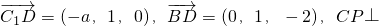 面BDC1,
面BDC1,∴
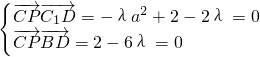 解得
解得
所以AA1=2,点P位置是在线段AB1上且
 .(12分)
.(12分)分析:(1)连接B1C,交BC1于点O,由三角形中位线定理,可得OD∥B1A,结合线面平行的判定定理可得AB1∥面BDC1;
(2)以C为坐标原点,CC1,CA,CB方向分别为X,Y,Z轴正方向建立空间坐标系,求出平面C1DB的法向量和平面BDC的法向量,代入向量夹角公式,即可求出二面角C1-BD-C的余弦值;
(3)设设
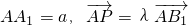 ,求出CP的方向向量和平面BDC1的法向量,根据CP⊥面BDC1,构造关于a,λ的方程组,解方程组,求出a,λ的值,即可得到AA1的长及点P的位置.
,求出CP的方向向量和平面BDC1的法向量,根据CP⊥面BDC1,构造关于a,λ的方程组,解方程组,求出a,λ的值,即可得到AA1的长及点P的位置.点评:本题考查的知识点是用空间向量求平面间的夹角,直线与平面平行的判定,直线与平面垂直的判定,其中(1)的关键是证得OD∥B1A,(2)(3)的关键是建立空间坐标系,将空间直线与平面的垂直关系及二面角问题转化为空间向量的夹角问题.

练习册系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=