题目内容
已知函数f(x)=4x3+3tx2-6t2x+t-1,x∈R,t∈R,
(1)当t≠0时,求f(x)的单调区间;
(2)证明:对任意的t∈(0,+∞),f(x)在区间(0,1)内均存在零点.
(1)当t≠0时,求f(x)的单调区间;
(2)证明:对任意的t∈(0,+∞),f(x)在区间(0,1)内均存在零点.
解:(1)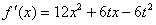 ,
,
令f′(x)=0,解得x=-t或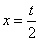 ,
,
①当t>0时,f′(x)>0的解集为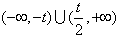 ;
;
∴f(x)的单调增区间为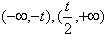 ,f(x)的单调减区间为
,f(x)的单调减区间为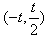 ;
;
②当t<0时,f′(x)<0的解集为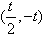 ,
,
∴f(x)的单调增区间为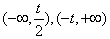 ,f(x)的单调减区间为
,f(x)的单调减区间为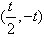 ;
;
(2)由(1)可知,当t>0时,f(x)在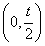 内单调递减,在
内单调递减,在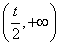 内单调递增,
内单调递增,
∴①当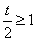 即t≥2时,f(x)在(0,1)内单调递减,在(1,+∞)单调递增,
即t≥2时,f(x)在(0,1)内单调递减,在(1,+∞)单调递增,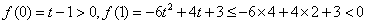 ,
,
所以对任意t∈[2,+∞),f(x)在区间(0,1)内均存在零点;
②当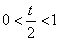 即0<t<2时,f(x)在
即0<t<2时,f(x)在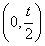 内单调递减,在
内单调递减,在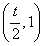 内单调递增,
内单调递增,
若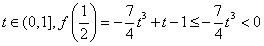 ,
,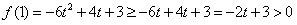 ,
,
所以f(x)在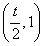 内存在零点;
内存在零点;
若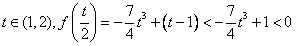 ,
,
f(0)=t-1>0,
所以f(x)在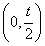 内存在零点;
内存在零点;
所以,对任意t∈(0,2),f(x)在区间(0,1)内均存在零点。
综上,对任意t∈(0,+∞),f(x)在区间(0,1)内均存在零点。

练习册系列答案
相关题目
已知函数f(x)=
,则它是( )
| ||
| |x-3|-3 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |