题目内容
设Sn为数列{an}的前n项和,Sn=kn2+n,n∈N*,其中k是常数,
(I)求a1及an;
(II)若对于任意的m∈N*,am,a2m,a4m成等比数列,求k的值。
解:(Ⅰ)当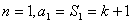 ,
,
当n≥2时,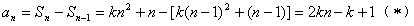
经检验,当n=1时,(*)式成立,
∴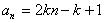 。
。
(Ⅱ)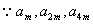 成等比数列,
成等比数列,
∴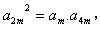
即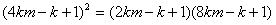 ,
,
整理,得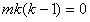 ,
,
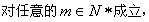
∴k=0或k=1。
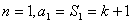 ,
,当n≥2时,
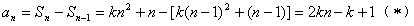
经检验,当n=1时,(*)式成立,
∴
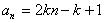 。
。(Ⅱ)
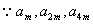 成等比数列,
成等比数列,∴
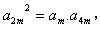
即
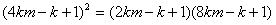 ,
,整理,得
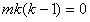 ,
,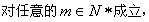
∴k=0或k=1。

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目