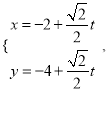题目内容
【题目】己知函数
（1）若
，
，求不等式
的解；
（2）对任意
，
，试确定函数
的最小值
（用含
，
的代数式表示），若正数、满足
，则、分别取何值时，有最小值，并求出此最小值.
【答案】（1）
；（2）
，
，
最小值为
.
【解析】
（1）根据题意，解不等式
，按
，
，
进行讨论，判断出绝对值的正负，解相应的不等式，得到答案；（2）按
，
，
，进行讨论，得到函数
的最小值，再将
转化为
，利用基本不等式求出的最小值，并求出此时
、
的值.
（1）函数
，代入
，
，
由
得
当时，
，解得
，所以
，
当时，
，解得
，所以，
当时，
，解得
，所以
，
综上，不等式的解集为
.
（2）因为
，
，
所以当时，
，
此时单调递减，所以
，
当时，
，
此时为常函数，所以
，
当时，
，
此时单调递增，所以
综上可得，的最小值
，
又因为，，且，即，
所以
，
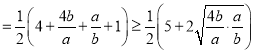
当且仅当
时，即
时，等号成立.
故当，，最小值为.
练习册系列答案
名校课堂系列答案
相关题目
