题目内容
已知函数f(x)=x3+ax2+bx+c在x=-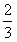 与x=1时都取得极值。
与x=1时都取得极值。
(1)求a、b的值与函数f(x)的单调区间。
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围。
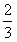 与x=1时都取得极值。
与x=1时都取得极值。(1)求a、b的值与函数f(x)的单调区间。
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围。
解:(1)f(x)=x3+ax2+bx+c,f'(x)=3x2+2ax+b
∴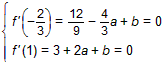 解得
解得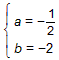
f'(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:

所以函数f(x)的递增区间是(-∞,-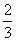 )∪(1,+∞),递减区间是(-
)∪(1,+∞),递减区间是(-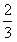 ,1)。
,1)。
(2)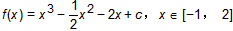
当x=-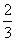 时,f(x)=
时,f(x)=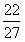 +c为极大值,而f(2)=2+c,所以f(2)=2+c为最大值
+c为极大值,而f(2)=2+c,所以f(2)=2+c为最大值
要使f(x)<c2对x∈[-1,2]恒成立,只需c2>f(2)=2+c
解得c<-1或c>2。
∴
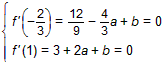 解得
解得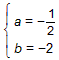
f'(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:

所以函数f(x)的递增区间是(-∞,-
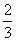 )∪(1,+∞),递减区间是(-
)∪(1,+∞),递减区间是(-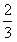 ,1)。
,1)。(2)
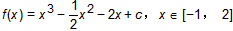
当x=-
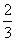 时,f(x)=
时,f(x)=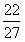 +c为极大值,而f(2)=2+c,所以f(2)=2+c为最大值
+c为极大值,而f(2)=2+c,所以f(2)=2+c为最大值要使f(x)<c2对x∈[-1,2]恒成立,只需c2>f(2)=2+c
解得c<-1或c>2。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|