题目内容
如图，在三棱锥V-ABC中，VC⊥底面ABC，AC⊥BC，D是AB的中点，且AC=BC=a，∠VDC=θ（0＜θ＜
）。
）。
（1）求证：平面VAB⊥平面VCD；
（2）试确定角θ的值，使得直线BC与平面VAB所成的角为
。
（2）试确定角θ的值，使得直线BC与平面VAB所成的角为
。解：（1）∵
，
∴
是等腰三角形，
又D是AB的中点，
∴
，
又
底面
∴
于是
平面
又
平面
，
∴平面
平面
。
（2） 过点C在平面
内作
于H，
则由（1）知
平面
连接
，于是
就是直线
与平面
所成的角
依题意
，
所以，在
中，
；
在
中，
，
∴
∵
，
∴
故当
时，直线BC与平面VAB所成的角为
。
，∴
是等腰三角形，又D是AB的中点，
∴
，又
底面∴
于是
平面又
平面，∴平面
平面。（2） 过点C在平面
内作于H，则由（1）知
平面连接
，于是就是直线与平面所成的角依题意
，所以，在
中，；在
中，，∴
∵
，∴
故当
时，直线BC与平面VAB所成的角为。
练习册系列答案
相关题目
如图，在三棱锥V-ABC中，VC⊥底面ABC，AC⊥BC，D是AB的中点，且AC=BC=a，∠VDC=θ（0＜θ＜
如图，在三棱锥V-ABC中，VC⊥底面ABC，AC⊥BC，D是AB的中点，且AC=BC=a，∠VDC=θ
如图，在三棱锥V-ABC中，VA⊥平面ABC，∠ABC=90°，且AC=2BC=2VA=4．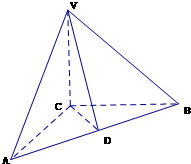
如图，在三棱锥V-ABC中，VC⊥底面ABC，AC⊥BC，D是AB的中点，且AC=BC=a，∠VDC=45°．
．