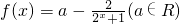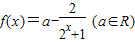题目内容

已知函数 $数学公式$
（1）判断下列三个命题的真假：
①f（x）是偶函数；②f（x）＜1；③当 $数学公式$ 时，f（x）取得极小值．
其中真命题有；（写出所有真命题的序号）
（2）满足 $数学公式$ 的正整数n的最小值为．

（1）证明：函数 $\text{[math]}$ 的定义域为x≠0，
当x≠0时， $\text{[math]}$ = $\text{[math]}$ =f（x），
∴f（x）是偶函数；①正确；
对于②，针对函数 $\text{[math]}$ 的性质，只须考虑当0＜x＜ $\text{[math]}$ 时的函数值即可，
如图，在单位圆中，有sinx=MA，
连接AN，则S_△OAN＜S_扇形OAN，
设 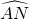$\text{[math]}$ 的长为l，则 $\text{[math]}$ ，
∴ $\text{[math]}$ ，即MA＜x，
又sinx=MA，
∴sinx＜x，∴ $\text{[math]}$ ，②正确；
$\text{[math]}$ = $\text{[math]}$
令 $\text{[math]}$ =0得xcosx-sinx=0，
即tanx=x，但当 $\text{[math]}$ 时，不满足tanx=x，
故当 $\text{[math]}$ 时，f（x）取不到极小值，故③错．
故答案为：①②．
（2）当n=1时， $\text{[math]}$ ， $\text{[math]}$ ，不满足 $\text{[math]}$ ；

当n=2时， $\text{[math]}$ ， $\text{[math]}$ ，不满足 $\text{[math]}$ ；
…
当n=8时， $\text{[math]}$ ， $\text{[math]}$ ，不满足 $\text{[math]}$ ；
当n=9时， $\text{[math]}$ ， $\text{[math]}$ ，满足 $\text{[math]}$ ．
故满足 $\text{[math]}$ 的正整数n的最小值为 9．
故答案为：9．
分析：（1）对于①，考察证明f（-x）与f（x）的关系得证；对于②针对函数 $\text{[math]}$ 的性质，只须考虑当0＜x＜ $\text{[math]}$ 时的函数值即可，再利用单位圆中的三角函数线，通过面积关系证明sinx＜x．对于③，利用商的导数运算法则及基本初等函数的导数公式，求出函数的导数，然后根据导函数的符号确定函数的单调性即可得到结论．
（2）分别令n=1，2，3，4，5，…，9．求出 $\text{[math]}$ 函数值，再比较大小即可得出答案．
点评：本小题主要考查利用导数研究函数的极值、函数单调性、函数奇偶性、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于中档题．