题目内容
在△ABC中,a=
 ,b=
,b= ,B=45°,则A等于( )
,B=45°,则A等于( )
| A.30° | B.60° | C.60°或120° | D.30°或150 |
C
解析试题分析:根据题意,由于在△ABC中,a=
 ,b=
,b= ,B=45°,那么由正弦定理可知
,B=45°,那么由正弦定理可知 ,因此可知角A的取值为60°或120°,故选C.
,因此可知角A的取值为60°或120°,故选C.
考点:正弦定理
点评:解决该试题的关键是根据已知中的两边和一边的对角可知采用正弦定理来求解三角形,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,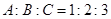 ,则
,则 等于( )
等于( )
A.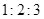 | B.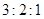 | C.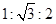 | D.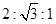 |
在 中,边
中,边 所对的角分别为
所对的角分别为 ,
,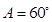 ,
, ,
, ,则
,则 解的情况为( )
解的情况为( )
| A.无解 | B.有一解 | C.有两解 | D.不能确定 |
在△ABC中,A=60°,C=45°,b=2,则此三角形的最小边长为( )
| A.2 | B.2 -2 -2 | C. -1 -1 | D.2( -1) -1) |
△ABC中,∠C=90°,且CA=CB=3,点M满足
 ,则
,则 =
=
| A.18 | B.3 | C.15 | D.9 |
在 中,若
中,若
 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知 中,
中, 所对的边分别为
所对的边分别为 ,且
,且 ,那么角
,那么角 等于( )
等于( )
A. | B. | C. | D. |
在△ 中,内角
中,内角 的对边分别为
的对边分别为 。若
。若 ,则
,则 =
=
A. | B. | C. | D. |
 的左右焦点,顶点P在双曲线C上,则
的左右焦点,顶点P在双曲线C上,则 得值等于( )
得值等于( ) (B)
(B)  (C)
(C)  (D)
(D) 