Question

如图，三棱柱ABC-A₁B₁C₁的侧面AA₁B₁B为正方形，侧面BB₁C₁C为菱形，∠CBB₁=60°，AB⊥B₁C．
（I）求证：平面AA₁B₁B⊥平面BB₁C₁C；
（II）求二面角B-AC-A₁的余弦值．

Answer 1

分析：（Ⅰ）利用线面、面面垂直的判定定理即可证明；
（Ⅱ）通过建立空间直角坐标系，利用两平面的法向量的夹角即可得到二面角．

解答：证明：（Ⅰ）由侧面AA₁B₁B为正方形，知AB⊥BB₁．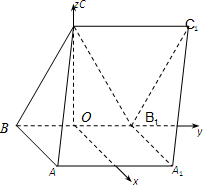
又AB⊥B₁C，BB₁∩B₁C=B₁，∴AB⊥平面BB₁C₁C，
又AB?平面AA₁B₁B，∴平面AA₁B₁B⊥BB₁C₁C．
（Ⅱ）由题意，CB=CB₁，设O是BB₁的中点，连接CO，则CO⊥BB₁．
由（Ⅰ）知，CO⊥平面AB₁B₁A．建立如图所示的坐标系O-xyz．
其中O是BB₁的中点，Ox∥AB，OB₁为y轴，OC为z轴．
不妨设AB=2，则A（2，-1，0），B（0，-1，0），C（0，0，

3

），A₁（2，1，0）．

AB

=（-2，0，0），

AC

=（-2，1，

3

），

AA1

=(0，2，0)．
设

n1

=（x₁，y₁，z₁）为面ABC的法向量，则

n1

•

AB

=0，

n1

•

AC

=0，
即

-2x1=0 -2x1+y1+ 3 z1=0

取z₁=-1，得

n1

=（0，

3

，-1）．
设

n2

=（x₂，y₂，z₂）为面ACA₁的法向量，则

n2

•

AA1

=0，

n2

•

AC

=0，
即

2y2=0 -2x2+y2+ 3 z2=0

取x₂=

3

，得

n2

=（

3

，0，2）．
所以cos?n₁，n₂＞=

n1• n2

| n1 | | n2 |

=-

7

7

．
因此二面角B-AC-A₁的余弦值为-

7

7

．

点评：熟练掌握线面、面面垂直的判定定理、通过建立空间直角坐标系并利用两平面的法向量的夹角求二面角的方法是解题的关键．