题目内容
用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
- A.

- B.

- C.

- D.20cm2
B
分析:设三角形的三边分别为a,b,c,令p= ,则p=10.海伦公式S=
,则p=10.海伦公式S= ≤
≤ =
= 故排除C,D,由于等号成立的条件为10-a=10-b=10-c,故“=”不成立,推测当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,进而得到答案.
故排除C,D,由于等号成立的条件为10-a=10-b=10-c,故“=”不成立,推测当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,进而得到答案.
解答:设三角形的三边分别为a,b,c,
令p= ,则p=10.由海伦公式S=
,则p=10.由海伦公式S=
知S= ≤
≤ =
= <20<3
<20<3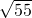
由于等号成立的条件为10-a=10-b=10-c,故“=”不成立,
∴S<20<3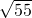 .
.
排除C,D.
由以上不等式推测,当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,此时三边长为7,7,6,用2、5连接,3、4连接各为一边,第三边长为7组成三角形,此三角形面积最大,面积为 ,
,
故选B.
点评:本题主要考查了三角形中的几何计算问题.题中巧妙的利用了海伦公式.
分析:设三角形的三边分别为a,b,c,令p=
 ,则p=10.海伦公式S=
,则p=10.海伦公式S= ≤
≤ =
= 故排除C,D,由于等号成立的条件为10-a=10-b=10-c,故“=”不成立,推测当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,进而得到答案.
故排除C,D,由于等号成立的条件为10-a=10-b=10-c,故“=”不成立,推测当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,进而得到答案.解答:设三角形的三边分别为a,b,c,
令p=
 ,则p=10.由海伦公式S=
,则p=10.由海伦公式S=
知S=
 ≤
≤ =
= <20<3
<20<3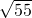
由于等号成立的条件为10-a=10-b=10-c,故“=”不成立,
∴S<20<3
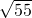 .
.排除C,D.
由以上不等式推测,当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,此时三边长为7,7,6,用2、5连接,3、4连接各为一边,第三边长为7组成三角形,此三角形面积最大,面积为
 ,
,故选B.
点评:本题主要考查了三角形中的几何计算问题.题中巧妙的利用了海伦公式.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为( )
A、8
| ||
B、6
| ||
C、3
| ||
| D、20cm2 |