题目内容
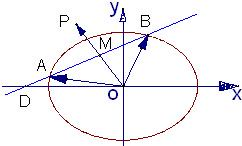
如图,已知椭圆
+y2=1,A、B为椭圆与x轴的交点,DA⊥AB,CB⊥AB,且|DA|=3
,|CB|=
,动点P在x轴上方的
上移动,则S△PCD的最小值______.
| x2 |
| 2 |
| 2 |
| 2 |
 |
| AB |

过点P作PH垂直x轴,并且交x轴于点H,
因为椭圆的方程为:
+y2=1,并且动点P在x轴上方的
上移动,
所以设点P(
cosθ,sinθ).
因为S梯形ABCD=
=8,并且S梯形ABCD=S梯形AHPD+S梯形HBCP+S△PCD,
所以若S△PCD最小,则S梯形AHPD+S梯形HBCP最大.
因为S梯形AHPD+S梯形HBCP=
+
=
sinθ+2cosθ+4=
sin(θ+α)+4,
所以由三角函数的性质可得:
sinθ+2cosθ+8的最大值为
+4,
所以S△PCD最小值为:8-(
+4)=4-
.
故答案为:4-
.
因为椭圆的方程为:
| x2 |
| 2 |
 |
| AB |
所以设点P(
| 2 |
因为S梯形ABCD=
(
| ||||||
| 2 |
所以若S△PCD最小,则S梯形AHPD+S梯形HBCP最大.
因为S梯形AHPD+S梯形HBCP=
(sinθ+3
| ||||||
| 2 |
(sinθ+
| ||||||
| 2 |
| 2 |
| 6 |
所以由三角函数的性质可得:
| 2 |
| 6 |
所以S△PCD最小值为:8-(
| 6 |
| 6 |
故答案为:4-
| 6 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知过点D(-2,0)的直线l与椭圆
如图,已知过点D(-2,0)的直线l与椭圆 如图,已知椭圆
如图,已知椭圆

 (2011•嘉定区三模)如图,已知椭圆
(2011•嘉定区三模)如图,已知椭圆