题目内容
 如图,已知椭圆
如图,已知椭圆| x2 |
| 2 |
| 2 |
| 2 |
 |
| AB |
4-
| 6 |
4-
.| 6 |
分析:过点P作PH垂直x轴,并且交x轴于点H,设点P(
cosθ,sinθ).由题意可得:S梯形ABCD=
=8,并且S梯形ABCD=S梯形AHPD+S梯形HBCP+S△PCD,若S△PCD最小,则S梯形AHPD+S梯形HBCP最大,再表示出两个梯形的面积和,进而利用三角函数的有关性质求出答案.
| 2 |
(
| ||||||
| 2 |
解答:解:过点P作PH垂直x轴,并且交x轴于点H,
因为椭圆的方程为:
+y2=1,并且动点P在x轴上方的
上移动,
所以设点P(
cosθ,sinθ).
因为S梯形ABCD=
=8,并且S梯形ABCD=S梯形AHPD+S梯形HBCP+S△PCD,
所以若S△PCD最小,则S梯形AHPD+S梯形HBCP最大.
因为S梯形AHPD+S梯形HBCP=
+
=
sinθ+2cosθ+4=
sin(θ+α)+4,
所以由三角函数的性质可得:
sinθ+2cosθ+8的最大值为
+4,
所以S△PCD最小值为:8-(
+4)=4-
.
故答案为:4-
.
因为椭圆的方程为:
| x2 |
| 2 |
 |
| AB |
所以设点P(
| 2 |
因为S梯形ABCD=
(
| ||||||
| 2 |
所以若S△PCD最小,则S梯形AHPD+S梯形HBCP最大.
因为S梯形AHPD+S梯形HBCP=
(sinθ+3
| ||||||
| 2 |
(sinθ+
| ||||||
| 2 |
| 2 |
| 6 |
所以由三角函数的性质可得:
| 2 |
| 6 |
所以S△PCD最小值为:8-(
| 6 |
| 6 |
故答案为:4-
| 6 |
点评:解决此类问题的关键是熟练掌握椭圆的参数方程与三角函数的有关性质,以及梯形的面积公式等知识点,此题综合性较强,属于难题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
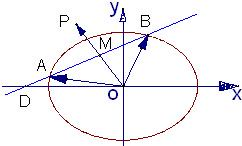 如图,已知过点D(-2,0)的直线l与椭圆
如图,已知过点D(-2,0)的直线l与椭圆
 (2011•嘉定区三模)如图,已知椭圆
(2011•嘉定区三模)如图,已知椭圆
