Question

       设有抛物线C：y= –x²+x–4，通过原点O作C的切线y=mx，使切点P在第一象限．

   （1）求m的值，以及P的坐标；

   （2）过点P作切线的垂线，求它与抛物线的另一个交点Q；

   （3）设C上有一点R，其横坐标为t，为使DOPQ的面积小于DPQR的面积，试求t的取值范围．

Answer 1

解：设点P的坐标为（x₁， y₁），则y₁=kx₁……①，y₁= –+x₁ – 4……②，

       ①代入②，得：+（k–）x₁+4=0…………………………………………………2分

       因为点P为切点，所以 （k–）²–16=0，得：k=或k=……………………4分

       当k=时x₁= －2，y₁= －17；当k=时，x₁= 2，y₁= 1；

       因为点P在第一象限，故所求的斜率k=，P的坐标为 （2，1），……………6分

   （2）过 P点作切线的垂线，其方程为：y=－2x+5……③，代入抛物线方程，得：

       x²－x+9=0，设Q点的坐标为 （x₂， y₂），则2x₂=9，所以x₂=，y₂=－4，

       所以Q点的坐标为 （，－4），………………………………………………10分

   （3）设C上有一点R（t，－t²+t–4），它到直线PQ的距离为：

       d=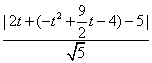=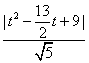……………………………………12分

       点O到直线PQ的距离PO =，S_DOPQ=´PQ´OP，S_DPQR=´PQ´d，

       因为DOPQ的面积小于DPQR的面积，S_DOPQ < S_DPQR ，

       即：OP < d，即：>5，……………………………………14分

       +4>0或+14<0

       解之得：t<或t>

       所以t的取值范围为t<或t>．……………………………16分