题目内容
已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是______________.

解析试题分析:由题意设棱长为a,补正三棱柱ABC-A2B2C2,构造直角三角形A2BM,解直角三角形求出BM,利用勾股定理求出A2M,从而求解.设棱长为a,补正三棱柱ABC-A2B2C2(如图)
平移 至
至 ,连接
,连接 ,∠MBA2即为
,∠MBA2即为 与
与 所成的角,
所成的角,
在△A2BM中,A2B= ,
, ,
, ,结合勾股定理∴
,结合勾股定理∴ 2+
2+ =
= 可知所求的角为
可知所求的角为 .故答案为
.故答案为
考点:异面直线所成的角
点评:此题主要考查了异面直线及其所成的角和勾股定理的应用,计算比较复杂,要仔细的做.

练习册系列答案
相关题目
 的棱长为1,
的棱长为1, 为
为 的中点,
的中点, 为线段
为线段 上的动点,过点
上的动点,过点 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为 ,则下列命题正确的是 (写出所有正确命题的编号)。
,则下列命题正确的是 (写出所有正确命题的编号)。
 时,
时, 时,
时, 时,
时, 的交点
的交点 满足
满足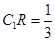
 时,
时, 时,
时,
 平面ABC,
平面ABC, ,给出下列结论:①
,给出下列结论:① ;②平面
;②平面 平面PBC;③直线
平面PBC;③直线 平面PAE;④
平面PAE;④ ;⑤直线PD与平面PAB所成角的余弦值为
;⑤直线PD与平面PAB所成角的余弦值为 。
。
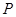 在正方体
在正方体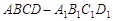 的面对角线
的面对角线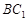 上运动,则下列四个命题:
上运动,则下列四个命题: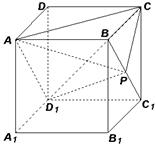
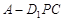 的体积不变;②
的体积不变;②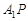 ∥平面
∥平面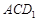 ;
;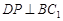 ;④平面
;④平面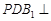 平面
平面 与矩形
与矩形 所在的平面互相垂直,将
所在的平面互相垂直,将 沿
沿 翻折,翻折后的点E恰与BC上的点P重合.设
翻折,翻折后的点E恰与BC上的点P重合.设 ,
, ,
, ,则当
,则当 __时,
__时, 有最小值.
有最小值.
 那么这条斜线与平面所成的角是 ____________
那么这条斜线与平面所成的角是 ____________