题目内容
(本小题满分14分)设函数 ,
, 的两个极值点为
的两个极值点为 ,线段
,线段 的中点为
的中点为 .
.
(1) 如果函数 为奇函数,求实数
为奇函数,求实数 的值;当
的值;当 时,求函数
时,求函数 图象的对称中心;
图象的对称中心;
(2) 如果 点在第四象限,求实数
点在第四象限,求实数 的范围;
的范围;
(3) 证明:点 也在函数
也在函数 的图象上,且
的图象上,且 为函数
为函数 图象的对称中心.
图象的对称中心.
(1)(1,0)
(2) 
(3)略
解析解:(1)【法一】因为 为奇函数,所以
为奇函数,所以 ,
,
得: .
.
当 时,
时, ,
,
有 ,则
,则 为奇函数. …………4分
为奇函数. …………4分
【法二】 ,
, 恒成立,
恒成立,  ,
,
求得 .
.
当 时,
时, ,该图象可由奇函数
,该图象可由奇函数 的图象向
的图象向
得:
 . …………9分
. …………9分
(3)由(2)得点 ,
,
又
= ,所以点
,所以点 也在函数
也在函数 的图象上.
的图象上.
【法一】 设
设 为函数
为函数 的图象上任意一点,
的图象上任意一点, 关于
关于 的对称点为
的对称点为
而

对称中心为 .
.
把函数 的图象按向量
的图象按向量 平移后得
平移后得 的图象,
的图象, 为函数
为函数 的对称中心. …………14分
的对称中心. …………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的极值;
的极值; 若函数
若函数 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数  的取值范围.
的取值范围. 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程 有三个根,它们分别为
有三个根,它们分别为 .
. ;
; 的取值范围.
的取值范围. , 其中
, 其中 为常数,且函数
为常数,且函数 图像过原点.
图像过原点.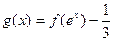 , 求函数
, 求函数 的零点
的零点 分)
分) .(
.( 为常数,
为常数, )
) 是函数
是函数 的一个极值点,求
的一个极值点,求 时,
时, 上是增函数;
上是增函数; ,总存在
,总存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 是奇函数
是奇函数 的定义域;
的定义域; 的值;
的值;
 时,求函数
时,求函数 在
在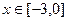 的值域;
的值域; 的方程
的方程 有解,求
有解,求 的取值范围
的取值范围