题目内容
.(14分)已知数列![]() 中,
中,![]() ,当
,当![]() 时,其前
时,其前![]() 项和
项和![]() 满足
满足![]() ,
,
求![]() 的表达式及
的表达式及![]() 的值;求数列
的值;求数列![]() 的通项公式;
的通项公式;
设![]() ,求证:当
,求证:当![]() 且
且![]() 时,
时,![]() .
.
(Ⅰ) -2  (Ⅱ) 略
(Ⅱ) 略
解析:
:(1)![]()
所以![]() 是等差数列.则
是等差数列.则![]() .
. .
.
当![]() 时,
时,![]() ,
,
综上, .
.
(2)令![]() ,当
,当![]() 时,有
时,有![]() (1)
(1)
法1:等价于求证 .
.
当![]() 时,
时,![]() 令
令![]()
![]() ,
,
则![]() 在
在![]() 递增.又
递增.又![]() ,所以
,所以![]() 即
即![]() .
.
法(2)![]()
![]() (2)
(2)
![]()
![]() (3)
(3)
因![]() ,所以
,所以![]()
由(1)(3)(4)知![]() .
.
法3:令![]() ,则
,则![]()
所以![]()
因![]() 则
则![]() ,
,![]()
所以![]() (5)由(1)(2)(5)知
(5)由(1)(2)(5)知![]()

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知数列 中,
中, ,当
,当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
 中,
中, ,且当
,且当 时,函数
时,函数 取得极值。
取得极值。 满足:
满足: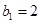 ,
, ,证明:
,证明: 是等差数列,并求数列
是等差数列,并求数列 项和
项和 .
.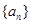 中,
中,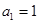 ,当
,当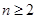 时,其前
时,其前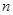 项和
项和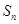 满足
满足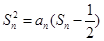
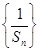 是等差数列;
是等差数列;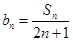 求
求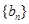 的前
的前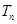 。
。 中,
中, ,当
,当 时,
时, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.