题目内容
满足A=30°，BC=10的△ABC恰好有不同两个，则边AB的长的取值范围为分析：如图，以B为圆心，10为半径做圆．不难看出，当圆B与AE相切于点C时，AB取得最大值为20，当圆B过点A时，
AB取得最小值为10，再结合三角形ABC有两个解，求得AB的范围．
AB取得最小值为10，再结合三角形ABC有两个解，求得AB的范围．
解答：解：如图所示：设∠DAE=30°，设B为AD上一动点，以B为圆心，10为半径做圆．
不难看出，当圆B与AE相切于点C时，AB取得最大值为20，此时三角形ABC有唯一解．
当圆B过点A时，AB取得最小值为10，此时三角形ABC有唯一解．
由于满足A=30°，BC=10的△ABC恰好有不同两个，故等号不成立，
故AB的范围为（10，20 ），
故答案为：（10，20）．
不难看出，当圆B与AE相切于点C时，AB取得最大值为20，此时三角形ABC有唯一解．
当圆B过点A时，AB取得最小值为10，此时三角形ABC有唯一解．
由于满足A=30°，BC=10的△ABC恰好有不同两个，故等号不成立，
故AB的范围为（10，20 ），
故答案为：（10，20）．
点评：本题考查解三角形问题，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
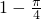； ②从200个元素中抽取20个样本，若采用系统抽样的方法则应分为10组，每组抽取2个； ③函数f（x）关于（3，0）点对称，满足f（6+x）=f（6-x），且当x∈[0，3]时函数为增函数，则f（x）在[6，9]上为减函数； ④满足A=30°，BC=1，
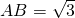的△ABC有两解．其中正确命题的个数为