题目内容
满足A=30°，BC=10的△ABC恰好有不同两个，则边AB的长的取值范围为________．
（10，20）
分析：根据30°＜C＜150°，可得
＜sinC＜1，由正弦定理解得AB=20sinC，可得 10＜AB＜20．
解答：∵A=30°，BC=10的△ABC恰好有不同两个，∴30°＜C＜150°，∴＜sinC＜1．
由正弦定理可得
，∴AB=20sinC，∴10＜AB＜20，
故边AB的长的取值范围为 （10，20），
故答案为：（10，20）．
点评：本题考查正弦定理，正弦函数的值域，不等式的性质，判断＜sinC＜1，是解题的关键．
分析：根据30°＜C＜150°，可得
＜sinC＜1，由正弦定理解得AB=20sinC，可得 10＜AB＜20．解答：∵A=30°，BC=10的△ABC恰好有不同两个，∴30°＜C＜150°，∴
＜sinC＜1．由正弦定理可得
，∴AB=20sinC，∴10＜AB＜20，故边AB的长的取值范围为 （10，20），
故答案为：（10，20）．
点评：本题考查正弦定理，正弦函数的值域，不等式的性质，判断
＜sinC＜1，是解题的关键． 
练习册系列答案
相关题目
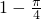； ②从200个元素中抽取20个样本，若采用系统抽样的方法则应分为10组，每组抽取2个； ③函数f（x）关于（3，0）点对称，满足f（6+x）=f（6-x），且当x∈[0，3]时函数为增函数，则f（x）在[6，9]上为减函数； ④满足A=30°，BC=1，
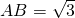的△ABC有两解．其中正确命题的个数为