题目内容
(本小题满分分)已知函数![]() (Ⅰ)求曲线
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若过点![]() 可作曲线
可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围.
的取值范围.
(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
解析:
:(1)![]() ………2分
………2分
∴曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() …4分
…4分
(2)过点![]() 向曲线
向曲线![]() 作切线,设切点为
作切线,设切点为![]()
则![]() 则切线方程为
则切线方程为![]() …6分
…6分![]()
整理得![]() ∵过点
∵过点![]() 可作曲线
可作曲线![]() 的三条切线
的三条切线
∴方程(*)有三个不同实数根.记![]()
令![]() 或1. …10分则
或1. …10分则![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大 |
| 极小 |
|
当![]() 有极大值
有极大值![]() 有极小值
有极小值![]() . …………12分
. …………12分
由![]() 的简图知,当且仅当
的简图知,当且仅当![]()
![]() 即
即![]() 时,
时,
函数![]() 有三个不同零点,过点
有三个不同零点,过点![]() 可作三条不同切线.
可作三条不同切线.
所以若过点![]() 可作曲线
可作曲线![]() 的三条不同切线,
的三条不同切线,![]() 的范围是
的范围是![]() ……14分
……14分

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
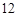 分)已知函数
分)已知函数 ,
,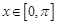 ,求该函数的单调递增区间。
,求该函数的单调递增区间。 分)
分) 的左、 右顶点分别为
的左、 右顶点分别为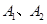 ,动直线
,动直线 与圆
与圆 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为 .
.
 的取值范围,并求
的取值范围,并求 的最小值;
的最小值; 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,那么,
,那么, 是定值吗?并证明
是定值吗?并证明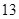 分)
分)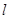 与抛物线
与抛物线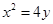 相切于点
相切于点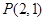 ,且与
,且与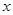 轴交于点
轴交于点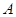 ,定点
,定点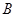 的坐标为
的坐标为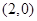 .
.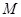 满足
满足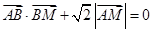 ,求点
,求点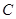 ;
;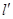 (斜率不等于零)与(I)中的轨迹
(斜率不等于零)与(I)中的轨迹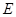 、
、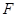 (
(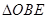 与
与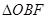 面积之比的取值范围.
面积之比的取值范围. 分)
分)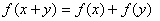 对于任何实数
对于任何实数 ,y都成立,
,y都成立, ;
; 的值;
的值; 为奇函数。
为奇函数。 分)
分)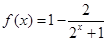 ,
, 的值域。
的值域。