题目内容
设数列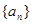 的首项为
的首项为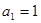 ,前n项和
,前n项和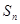 满足关系式:
满足关系式:
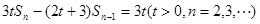
1)求证: 数列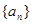 是等比数列;
是等比数列;
2)设数列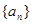 的公比为f(t),作数列
的公比为f(t),作数列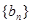 ,使得
,使得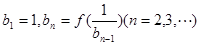 ,求:b
,求:b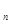 及
及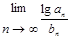 ;
;
3)求和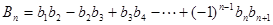 。
。
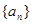 的首项为
的首项为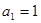 ,前n项和
,前n项和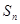 满足关系式:
满足关系式: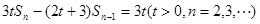
1)求证: 数列
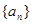 是等比数列;
是等比数列; 2)设数列
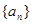 的公比为f(t),作数列
的公比为f(t),作数列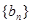 ,使得
,使得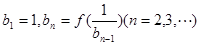 ,求:b
,求:b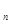 及
及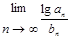 ;
;3)求和
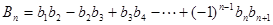 。
。1)可求得 。
。
2)b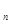 ="2n/3+1/3,"
="2n/3+1/3," 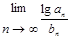 =
= ;
;
3)
 。
。2)b
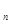 ="2n/3+1/3,"
="2n/3+1/3," 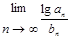 =
= ;
;3)

本题主要考查了等比关系的确定.考查了学生综合分析问题的能力.
(1)由 求得数列{an}的递推式,进而来判定数列
求得数列{an}的递推式,进而来判定数列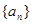 是等比数列;
是等比数列;
(2)把f(t)的解析式代入bn,进而可知bn=1+bn-1,判断出{bn}是一个首项为1,公差为2/3的等差数列.进而根据等差数列的通项公式求得答案.
(3){bn}是等差数列.进而可推断出{b2n-1}和{b2n}也是首项分别为1和2,公差均为2的等差数列,进而用分组法求得数列的 和
和
(1)由
 求得数列{an}的递推式,进而来判定数列
求得数列{an}的递推式,进而来判定数列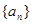 是等比数列;
是等比数列;(2)把f(t)的解析式代入bn,进而可知bn=1+bn-1,判断出{bn}是一个首项为1,公差为2/3的等差数列.进而根据等差数列的通项公式求得答案.
(3){bn}是等差数列.进而可推断出{b2n-1}和{b2n}也是首项分别为1和2,公差均为2的等差数列,进而用分组法求得数列的
 和
和
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
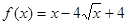 (x≥4)的反函数为
(x≥4)的反函数为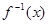 ,数列
,数列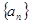 满足:a1=1,
满足:a1=1,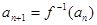 ,(
,(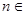 N*),数列
N*),数列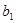 ,
,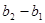 ,
,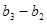 ,…,
,…,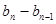 是首项为1,公比为
是首项为1,公比为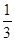 的等比数列.
的等比数列.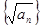 为等差数列; (Ⅱ)若
为等差数列; (Ⅱ)若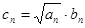 ,求数列
,求数列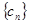 的前n项和
的前n项和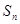 .
. } 是公比为2的等比数列,且a 7 =" 16" ,则
} 是公比为2的等比数列,且a 7 =" 16" ,则 =( )
=( ) 的离心率是( )
的离心率是( )


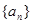 满足
满足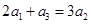 ,且
,且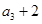 是
是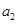 与
与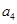 的等差中项;
的等差中项;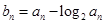 ,
,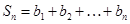 ,
,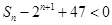 成立的
成立的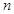 的最小值;
的最小值;  ,a4=-4,则|a1|+|a2|+…+|an|=( )
,a4=-4,则|a1|+|a2|+…+|an|=( )



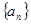 中,
中, 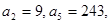 则
则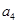 = ( )
= ( ) 中,
中, ,
, ,
, 成等差数列, 则
成等差数列, 则 ( )
( ) 


