已知圆C1:(x-1)2+(y-1)2=1.圆C2:(x-3)2+(y-2)2=4.动点P在x轴上.动点M.N分别在圆C1和圆C2上.则|PM|+|PN|的最小值是$\sqrt{13}$-3．题目和参考答案——青夏教育精英家教网—

题目内容

5．已知圆C₁：（x-1）²+（y-1）²=1，圆C₂：（x-3）²+（y-2）²=4，动点P在x轴上，动点M，N分别在圆C₁和圆C₂上，则|PM|+|PN|的最小值是$\sqrt{13}$-3．

分析根据题意画出图形，结合图形，求出圆C₁关于x轴的对称圆的圆心坐标A与半径，再求出圆A与圆C₂的圆心距减去两个圆的半径和，即为|PM|+|PN|的最小值．

解答解：如图所示，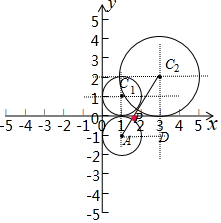

圆C₁关于x轴的对称圆的圆心坐标A（1，-1），半径为1，
圆C₂的圆心坐标C₂（3，2），半径为2，
连接AC₂，故|AC₂|=$\sqrt{4+9}$=$\sqrt{13}$，
故|PM|+|PN|的最小值是$\sqrt{13}$-3
故答案为：$\sqrt{13}$-3．

点评本题考查圆的对称圆方程以及两圆的位置关系，两点距离公式的应用问题，也考查了转化思想与计算能力，数形结合思想的应用问题，是综合性题目．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

16．设集合A={-1，0，1}，B={x|x²-2x-3＜0}，则A∩B=（　　）

13．已知点M（-lna，0），N（lna，0），其中a＞1，若圆C：x²+（y-2）²=1上不存在点P，使得∠MPN=90°，则实数a的取值范围是（1，e）∪（e³，+∞）．

20．已知函数f（x）=ax+$\frac{1}{{x}^{2}}$（a∈R）．
（Ⅰ）讨论函数f（x）的奇偶性，并说明理由；
（Ⅱ）若函数f（x）在x∈[2，+∞）上为增函数，求实数a的取值范围．

10．把二进制数101001_（2）化为十进制数为41．

4．偶函数y=f（x），x∈R，当x＜0时，y=f（x）是增函数，若|x₁|＜|x₂|，且x₁＜0，x₂＞0．（　　）

1．已知向量$\vec m$=（$\sqrt{3}$sinx，sinx），$\vec n$=（cosx，sinx）．
（1）若$\vec m∥\vec n$且$x∈[{0，\frac{π}{2}}]$，求角x；
（2）若f（x）=$\overrightarrow m•\overrightarrow n$，函数g（x）=f（x+$\frac{π}{12}$），求函数g（x）的最小正周期和单调递增区间．

2．下列说法正确的是（　　）

	A．	在统计学中，回归分析是检验两个分类变量是否有关系的一种统计方法
	B．	线性回归方程对应的直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$至少经过其样本数据点（x₁，y₁），（x₂，y₂），（x₃，y₃），（x_n，y_n）中的一个点
	C．	在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高
	D．	在回归分析中，相关指数R²为0.98的模型比相关指数R²为0.80的模型拟合的效果差

试题分类