题目内容
把函数y=f(x)在x=a及x=b之间的一段图像近似地看作直线，设a≤c≤b，证明f(c)的近似值是：f(a)+
［f(b)-f(a)］.
证明:如图4,依题意,点M、N的坐标分别为(a,f(a))、(b,f(b)),
图4
所以直线MN的方程为y-f(a)=
(x-a),其中a≤x≤b.
因为a≤c≤b,所以当x=c时,有y=f(a)+
(c-a).
因为在x=a,x=b之间的一段图像可以近似地看作直线,
所以有f(c)≈f(a)+
(c-a),
即f(c)的近似值为f(a)+
［f(b)-f(a)］.
练习册系列答案
一本好题口算题卡系列答案
相关题目
)内的
两个零点x1，x2，求x1 + x2的值；
向左平移m (m＞0)个单位使所得函数的图象关于点(0，2)对称，求m的最小值．
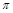)内的两个零点x1，x2，求x1 + x2的值；