Question

已知函数f (x) = 2cos²x-2sinxcosx + 1．

（1）设方程f (x) – 1 = 0在(0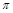，)内的两个零点x₁，x₂，求x₁ + x₂的值；

（2）把函数y = f (x)的图象向左平移m (m＞0)个单位使所得函数的图象关于点(0，2)对称，求m的最小值．

 

 

Answer 1

【答案】

 

 

1）由题设得f (x) = –sin2x + 1 + cos2x + 1 =      ………2分

    ∵f (x) – 1 = 0，∴        ………3分

    由．得…5分

    ∵                      ……………6分

    （2）设y = f (x)的图象向左平移m个单位，得到函数g (x)的图象，

 则                                     …………………8分

∵y = g (x)的图象关于点(0，2)对称，∴…………10分

∴

∵m＞0，∴当k = 0时，m取得最小值．           ………13分

 

【解析】略