题目内容
在△ABC 中，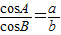
，则△ABC一定是（ ）A．等腰三角形
B．直角三角形
C．等腰直角三角形
D．等边三角形
【答案】分析：把已知的等式利用正弦定理化简，再利用同角三角函数间的基本关系得到tanA与tanB相等，根据A和B都为三角形的内角，得到A与B相等，根据等角对等边得到a=b，即三角形ABC为等腰三角形．
解答：解：根据正弦定理：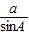
=
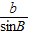化简已知等式得：
=
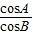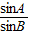，即tanA=tanB，
由A和B都为三角形的内角，得到A=B，
则△ABC一定为等腰三角形．
故选A
点评：此题考查了三角函数中的恒等变换应用，以及正弦定理．学生做题时注意角度A和B都为三角形的内角这个条件．
解答：解：根据正弦定理：
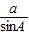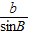=化简已知等式得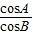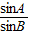：=，即tanA=tanB，由A和B都为三角形的内角，得到A=B，
则△ABC一定为等腰三角形．
故选A
点评：此题考查了三角函数中的恒等变换应用，以及正弦定理．学生做题时注意角度A和B都为三角形的内角这个条件．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
,则这个三角形是( ) 
则
( )
B．
C．
D．
,
,
,则角
的大小为
（ ）
或
B．
或
C．
ABC中，
，则三角形的形状为（ ）
，则k的值是（ ）
D．