题目内容
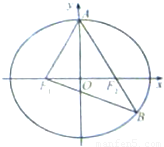
如图,F1、F2分别是椭圆C: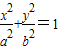 (a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.(Ⅰ)求椭圆C的离心率;
(Ⅱ)已知△AF1B的面积为40
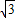 ,求a,b 的值.
,求a,b 的值.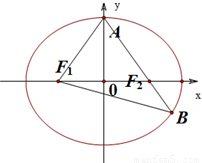
【答案】分析:(Ⅰ)直接利用∠F1AF2=60°,求椭圆C的离心率;
(Ⅱ)设|BF2|=m,则|BF1|=2a-m,利用余弦定理以及已知△AF1B的面积为40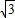 ,直接求a,b 的值.
,直接求a,b 的值.
解答:解:(Ⅰ)∠F1AF2=60°?a=2c?e=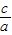 =
= .
.
(Ⅱ)设|BF2|=m,则|BF1|=2a-m,
在三角形BF1F2中,|BF1|2=|BF2|2+|F1F2|2-2|BF2||F1F2|cos120°
?(2a-m)2=m2+a2+am.?m=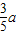 .
.
△AF1B面积S= |BA||F1F2|sin60°
|BA||F1F2|sin60°
?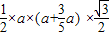 =40
=40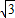
?a=10,
∴c=5,b=5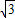 .
.
点评:本题考查椭圆的简单性质,余弦定理的应用,考查计算能力.
(Ⅱ)设|BF2|=m,则|BF1|=2a-m,利用余弦定理以及已知△AF1B的面积为40
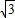 ,直接求a,b 的值.
,直接求a,b 的值.解答:解:(Ⅰ)∠F1AF2=60°?a=2c?e=
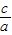 =
= .
.
(Ⅱ)设|BF2|=m,则|BF1|=2a-m,
在三角形BF1F2中,|BF1|2=|BF2|2+|F1F2|2-2|BF2||F1F2|cos120°
?(2a-m)2=m2+a2+am.?m=
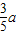 .
.△AF1B面积S=
 |BA||F1F2|sin60°
|BA||F1F2|sin60°?
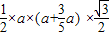 =40
=40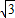
?a=10,
∴c=5,b=5
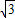 .
.点评:本题考查椭圆的简单性质,余弦定理的应用,考查计算能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 如图,F1,F2分别为双曲线
如图,F1,F2分别为双曲线 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 的左、右焦点,点P在椭圆上,△POF2是面积
的左、右焦点,点P在椭圆上,△POF2是面积 的正三角形,则
的正三角形,则 的值是
的值是