题目内容
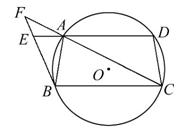
如图,☉O和☉O′相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交☉O于点E.证明:
(1)AC·BD=AD·AB.
(2)AC=AE.
【证明】(1)由AC与圆O′相切于点A,
得∠CAB=∠ADB,同理,∠ACB=∠DAB,
从而△AC
B∽△DAB,
所以
=
AC·BD=AD·AB.
(2)由AD与圆O相切于点A,得∠AED=∠BAD.
又∠ADE=∠BDA,从而△EAD∽△ABD,所以
=
AE·BD=AB·AD.
又由(1)知,AC·BD=AB·AD.
所以AC·BD=AE·BD,∴AC=AE.
练习册系列答案
相关题目
B的中点,AD的延长线交☉O于点E,则线段D
(B)
(C)
(D)
