题目内容
甲、乙两位歌手在“中国好声音”选拔赛中，5位评委评分情况如茎叶图所示，记甲、乙两人的平均得分分别为. |
| x甲 |
. |
| x乙 |
分析：根据茎叶图的数据，利用平均值和数值分布情况进行判断即可．
解答：解：由茎叶图知，甲的得分情况为17，16，28，30，34；
乙的得分情况为15，28，26，28，33，
因此可知甲的平均分为
=
(77+76+88+90+94)=85，
乙的平均分为
=
(75+86+88+88+93)=86，
故可知
＜
，排除C、D，
同时根据茎叶图数据的分布情况可知，乙的数据主要集中在86左右，甲的数据比较分散，
乙比甲更为集中，故乙比甲成绩稳定，选B．
故选B．
乙的得分情况为15，28，26，28，33，
因此可知甲的平均分为
. |
| x甲 |
| 1 |
| 5 |
乙的平均分为
. |
| x乙 |
| 1 |
| 5 |
故可知
. |
| x甲 |
. |
| x乙 |
同时根据茎叶图数据的分布情况可知，乙的数据主要集中在86左右，甲的数据比较分散，
乙比甲更为集中，故乙比甲成绩稳定，选B．
故选B．
点评：本题主要考查茎叶图的应用，以及平均数的求法要求熟练掌握相应的概念和公式，考查学生的计算能力．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
某电视台举办了“中华好声音”大型歌手选秀活动，过程分为初赛、复赛和决赛，经初赛进入复赛的40名选手被平均分成甲、乙两个班，由组委会聘请两位导师各负责一个班进行声乐培训。下面是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图：
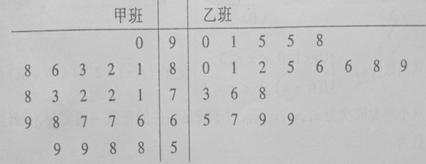
赛制规定：参加复赛的40名选手中，获得的支持票数排在前5名的选手可进入决赛，若第5名出现并列，则一起进入决赛；另外，票数不低于95票的选手在决赛时拥有“优先挑战权”。
1、从进入决赛的选手中随机抽出3名，求其中恰有1名拥有“优先挑战权”的概率；
2、电视台决定，复赛票数不低于85票的选手将成为电视台的“签约歌手”，请填写下面的2×2列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关？
|
|
甲班 |
乙班 |
合计 |
|
签约歌手 |
|
|
|
|
末签约歌手 |
|
|
|
|
合计 |
|
|
|
下面临界值表仅供参考：
|
P（K2≥k） |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式：K2=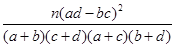
,其中
.如图所示的茎叶图是青年歌手电 甲 乙 