题目内容
已知双曲线 的离心率为2,点A(a,0),B(0,-b),若原点到直线AB的距离为
的离心率为2,点A(a,0),B(0,-b),若原点到直线AB的距离为 ,则该双曲线两准线间的距离等于
,则该双曲线两准线间的距离等于
- A.

- B.

- C.1
- D.2
C
分析:先根据离心率为2得到a和c之间的关系,再结合点A(a,0),B(0,-b),以及原点到直线AB的距离为 ,求出a,b,c即可得到结论.
,求出a,b,c即可得到结论.
解答:因为:离心率为2
所以: =2?c=2a?c2=4a2=a2+b2?b=
=2?c=2a?c2=4a2=a2+b2?b= a.
a.
直线AB的方程为:bx-ay-ab=0
所以有: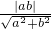 =
= ?b=
?b= ,a=1,c=2.
,a=1,c=2.
故: -(-
-(- )=
)= =1.
=1.
故选C.
点评:本题主要考查双曲线的性质应用.解决这类问题的关键在于对性质的熟练掌握以及灵活运用.
分析:先根据离心率为2得到a和c之间的关系,再结合点A(a,0),B(0,-b),以及原点到直线AB的距离为
 ,求出a,b,c即可得到结论.
,求出a,b,c即可得到结论.解答:因为:离心率为2
所以:
 =2?c=2a?c2=4a2=a2+b2?b=
=2?c=2a?c2=4a2=a2+b2?b= a.
a.直线AB的方程为:bx-ay-ab=0
所以有:
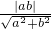 =
= ?b=
?b= ,a=1,c=2.
,a=1,c=2.故:
 -(-
-(- )=
)= =1.
=1.故选C.
点评:本题主要考查双曲线的性质应用.解决这类问题的关键在于对性质的熟练掌握以及灵活运用.

练习册系列答案
相关题目
已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 的离心率为2,焦点到渐近线的距离等于
的离心率为2,焦点到渐近线的距离等于 ,过右焦点
,过右焦点 的直线
的直线
 、
、 两点,
两点, 为左焦点,
为左焦点, 的面积等于
的面积等于 ,求直线
,求直线 的方程.
的方程. 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为 ,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
 (O为坐标原点),求t的取值范围
(O为坐标原点),求t的取值范围