题目内容
【题目】已知曲线C上每一点到直线l：
的距离比它到点
的距离大1.
（1）求曲线C的方程；
（2）曲线C任意一点处的切线m（不含x轴）与直线
相交于点M，与直线l相交于点N，证明：
为定值，并求此定值.
【答案】（1）
；（2）证明见解析，
为定值0.
【解析】
（1）利用抛物线的定义可得曲线
是顶点在原点，
轴为对称轴，
为焦点的抛物线，从而求出曲线的方程；
（2）依题意，切线
的斜率存在且不等于0，设切线的方程为：
，与抛物线方程联立，利用△
得到
，故切线的方程可写为
，进而求出点
，
的坐标，用坐标表达出
和
，即可证得
为定值．
解：（1）由题意可知，曲线C上每一点到直线
的距离等于该点到点
的距离，
曲线C是顶点在原点，y轴为对称轴，为焦点的抛物线.
曲线C的轨迹方程为：.
（2）依题设，切线m的斜率存在且不等于零，设切线m的方程为
（
），
代入得
，即
.
由
得
，化简整理得.
故切线m的方程可写为.
分别令
，
得M，N的坐标为
，
，
，
.
.
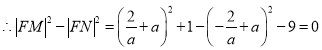即为定值0.
练习册系列答案
相关题目
