题目内容
设a为实数,函数f(x)=x3-ax2+(a2-1)x在(-∞,0)和(1,+∞)上都是增函数,求a的取值范围.
解:f′(x)=3x2-2ax+(a2-1),
其判别式△=4a2-12a2+12=12-8a2,
(1)若△=12-8a2=0,即 ,
,
当 或
或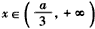 时,f′(x)>0,f(x)在(-∞,+∞)上为增函数,
时,f′(x)>0,f(x)在(-∞,+∞)上为增函数,
所以 。
。
(2)若△=12-8a2<0,恒有f′(x)>0,f(x)在(-∞,+∞)上为增函数,
所以 ,即
,即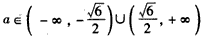 ;
;
(3)若 ,即
,即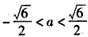 ,
,
令f′(x)=0,解得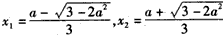 ,
,
当x∈(-∞,x1)或x∈(x2,+∞)时,f′(x)>0,f(x)为增函数;
当x∈(x1,x2)时,f′(x)<0,f(x)为减函数,
依题意x1≥0且x2≤1,
由x1≥0得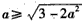 ,解得
,解得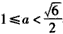 ;
;
由x2≤1得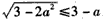 ,解得
,解得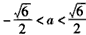 ;
;
从而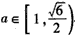 ;
;
综上,a的取值范围为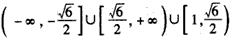 ,
,
即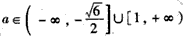 。
。
其判别式△=4a2-12a2+12=12-8a2,
(1)若△=12-8a2=0,即
 ,
,当
 或
或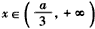 时,f′(x)>0,f(x)在(-∞,+∞)上为增函数,
时,f′(x)>0,f(x)在(-∞,+∞)上为增函数,所以
 。
。(2)若△=12-8a2<0,恒有f′(x)>0,f(x)在(-∞,+∞)上为增函数,
所以
 ,即
,即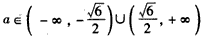 ;
;(3)若
 ,即
,即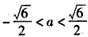 ,
,令f′(x)=0,解得
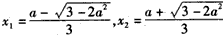 ,
,当x∈(-∞,x1)或x∈(x2,+∞)时,f′(x)>0,f(x)为增函数;
当x∈(x1,x2)时,f′(x)<0,f(x)为减函数,
依题意x1≥0且x2≤1,
由x1≥0得
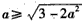 ,解得
,解得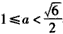 ;
;由x2≤1得
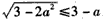 ,解得
,解得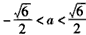 ;
;从而
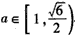 ;
;综上,a的取值范围为
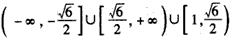 ,
,即
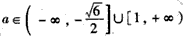 。
。 
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目