Question

【题目】某班20名同学某次数学测试的成绩可绘制成如下茎叶图，由于其中部分数据缺失，故打算根据茎叶图中的数据估计全班同学的平均成绩.

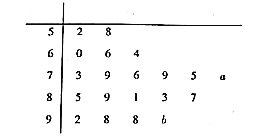
(1)完成频率分布直方图；

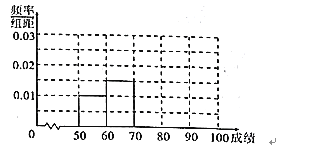
(2)根据(1)中的频率分布直方图估计全班同学的平均成绩 (同一组中的数据用该组区间的中点值作代表)；

(3)设根据茎叶图计算出的全班的平均成绩为，并假设，且各自取得每一个可能值的机会相等，在(2)的条件下，求概率.

Answer 1

【答案】(1)见解析 ;(2) 78分；（3）.

【解析】试题分析：（1）结合茎叶图，频率等于，求出画出频率分布直方图即可；（2）根据频率分布直方图，求出平均数 即可；（3）根据茎叶图计算出的全班的平均成绩为y，得到关于a与b的不等式，因为,利用古典概型求出概率．

试题解析：

(1)频率分布直方图如下：

(2) ，

即全班同学平均成绩可估计为78分.

(3) ，

故,因为

共有36种情况，符合的有（2,2）（2,3）（3,2）三种情况，故.